Review paper on depth, qubits and $T$ gates number on Clifford+T decomposition for various "typical" algorithms

Question

My question

I am looking for some review paper, or a list of different papers providing concrete numbers about the depth, number of qubits and number of $T$ gates required on the Clifford+T basis for usefull quantum algorithms (quantum Fourier transform, Grover, HHL, any other you can think of).

I am not looking for asymptotic behaviors as I would like to have an idea of the concrete numbers for typical problem sizes. This question is "simple" but I haven't found any paper summarizing it nicely so far, and there are some papers providing only half of the numbers required (for instance the number of qubits but not the depth).

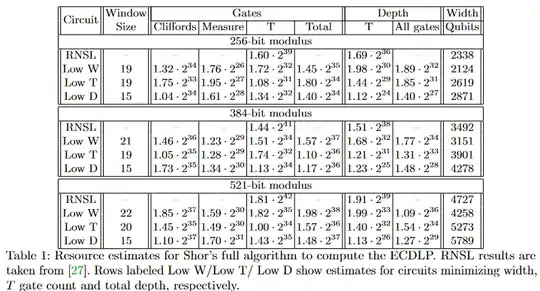
I am in particular interested to find "powerfull algorithms" in the regime where: $Q_L N_L \leq 10^{11}$, where $Q_L$ and $D_L$ are the number of logical qubits, and the logical depth of the algorithm. Typically Shor algorithm applied for RSA 2048 is often given as an example of powerful quantum algorithm. But it requires quite a lot of resources, I am looking for usefull algorithms requiring less than Shor (more precisely in the regime I just provided).

Further information

As suggested in the comment, it may happen that for some algo, the answer will depend on some extra characteristics describing the problem. In such case, one specific example would be fine for me as long as it outperforms the best known classical algo dedicated to solve the same task. Again I just would like to have some rough idea of the number of $T$ gates, qubits and depth required for a quantum algorithm clearly outperforming the best known classical algorithm solving the same task.

The reason why I am looking for Clifford+T decomposition is because I want to know the values for fault-tolerant quantum computing. However ideally, I don't want the paper to already assume which scheme of fault-tolerance I use to implement those gates. I already know how I implement them on my side, I really just need to know the (logical) depth, number of qubits and $T$ gates strictly required by the algorithm assuming I know how to implement $T$ and Clifford. I don't need any restriction in connectivity neither (like nearest neighbor interactions).

As last comment: I know that some of the answer will say "it depends", for instance it depends on how accurate we want the decomposition of the algorithm on the gateset (we can only approximate unitaries with Clifford+T). But anyway in practice to solve a concrete task we can find a reasonably good approximation. I am looking for a kind of source that thought about all this already.

Some references I already found

• Approximate QFT

This paper provides concrete numbers for everything but the algorithm depth that is lacking.

• Derivative pricing

This paper given in the comments provides good numbers, but it is not really outperforming what is doable on classical computers (see comments).

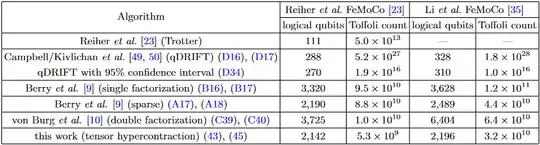
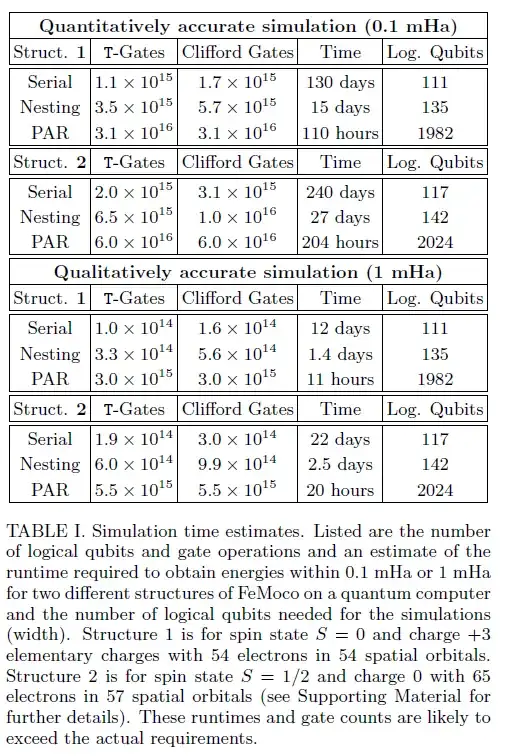
• Computing electromagnetic scattering cross section

This paper provides everything, but the depth is extremly high (typically $10^{20}$ way beyond the regime I am interested in).

Answer 1

Copying over from "Are circuits with more than 1000 gates common?". Note that a Toffoli gate is roughly as expensive as 2T gates or 4T gates, depending on your architecture.

According to Table III of https://arxiv.org/abs/2011.03494 , quantum chemistry algorithms looking at properties of the FeMoCo molecule use half a billion Toffoli gates.

According to Table 1 of https://arxiv.org/abs/1905.09749 , factoring 2048 bit numbers takes 3 billion Toffoli gates:

According to Table 1 of https://arxiv.org/abs/2001.09580 , 256 bit elliptic curve discrete logarithms take a few billion T gates:

Answer 2

The most useful use-case I found for a big fault-tolerant quantum computer, besides Shor, is a simulation of molecules, which are too hard to simulate on classical computers + demand fault-tolerant computers.

Read this article

Generally speaking, you can see the following demand (depending on the accuracy you want):

The approximation that they are doing about the number of physical qubits, is ok that this is just approximation because it depends on noise and coding, which is ok to be talked separately not in this context when showing a new algorithm application.