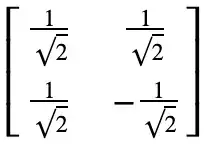The Qiskit standard gate list
You can find the full list of Qiskit standard gates in the module qiskit.circuit.library.standard_gates (documentation).
The matrix representation of a standard gate
For each gate, you can see its matrix representation with the to_matrix method. For example:
from qiskit.circuit.library import standard_gates
standard_gates.HGate().to_matrix()
array([[ 0.70710678+0.j, 0.70710678+0.j],
[ 0.70710678+0.j, -0.70710678+0.j]])
Or, its latex representation:
from qiskit.visualization import array_to_latex
array_to_latex(standard_gates.HGate().to_matrix())
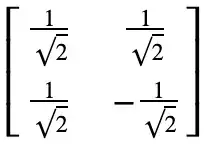
Creating your own custom gate
You can create your own gates from a circuit. For example:
from qiskit import QuantumCircuit
custom_circuit = QuantumCircuit(2, name='bell')
custom_circuit.h(0)
custom_circuit.cx(0, 1)
custom_gate = custom_circuit.to_gate()
You can create a circuit using that custom gate:
circuit = QuantumCircuit(3)
circuit.h(0)
circuit.append(custom_gate, [0,1])
circuit.cx(1, 2)
circuit.draw()
┌───┐┌───────┐
q_0: ┤ H ├┤0 ├─────
└───┘│ bell │
q_1: ─────┤1 ├──■──
└───────┘┌─┴─┐
q_2: ──────────────┤ X ├
└───┘
Telling the transpiler not to decompose your custom gate
Following the previous example, you can transpile that circuit using the custom gate name in the target basis list:
from qiskit.compiler import transpile
basis_gates = ['bell', 'u3', 'cx']
qc_trans = transpile(circuit, basis_gates=basis_gates)
qc_trans.draw()
┌─────────────┐┌───────┐
q_0: ┤ U3(π/2,0,π) ├┤0 ├─────
└─────────────┘│ bell │
q_1: ───────────────┤1 ├──■──
└───────┘┌─┴─┐
q_2: ────────────────────────┤ X ├
└───┘
Your custom gate as basis target of a circuit that is not using it
You can basis-target your own custom in some cases. That requires to extend the equivalence library. Following your mycx example:
- Create a circuit definition with your custom gate
mycx = QuantumCircuit(2, name='mycx')
mycx.cx(0, 1)
mycx_def = QuantumCircuit(2)
mycx_def.append(mycx.to_gate(), [0, 1])
- Add an equivalence to the library where a gate (
CXGate in this case) is equivalent to that definition.
StandardEquivalenceLibrary.add_equivalence(CXGate(), mycx_def)
- Create a circuit that uses the domain gate (
CXGate in this case).
from qiskit.compiler import transpile
qc = QuantumCircuit(3)
qc.h(0)
qc.cx(0, 1)
qc.cx(1, 2)
- Transpile using the parameter
translation_method='translator'. This will tell the transpiler to use the equivalence library for basis translation. In the basis_gate parameter you can refer to your custom gate name (mycx in this case):
result = transpile(qc, basis_gates=['mycx', 'u3'], translation_method='translator')
result.draw()
┌─────────────┐┌───────┐
q_0: ┤ U3(π/2,0,π) ├┤0 ├─────────
└─────────────┘│ mycx │┌───────┐
q_1: ───────────────┤1 ├┤0 ├
└───────┘│ mycx │
q_2: ────────────────────────┤1 ├
└───────┘