Partial Cyclic Permutation with only Toffoli and CNOT gates?

Question

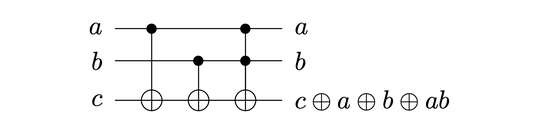
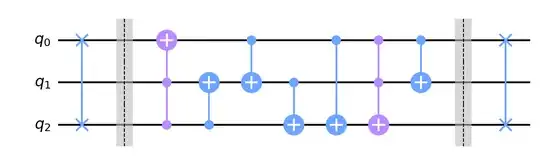
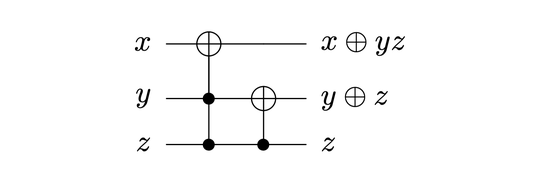I have been trying to solve this puzzle of constructing this transformation from CNOT and Toffoli gates as mentioned in NC page 193 (Ex 4.27)

Here is what I have done:

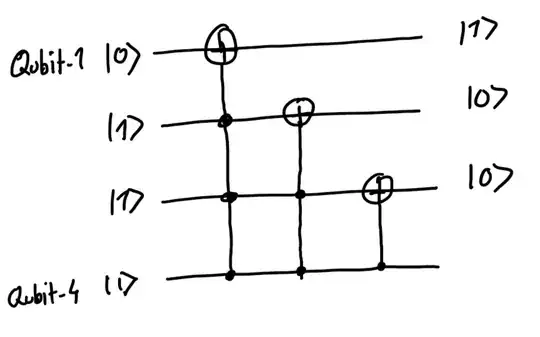
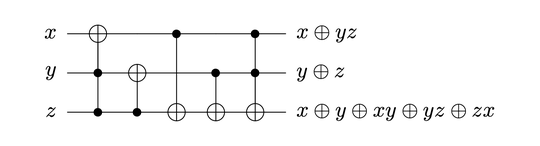
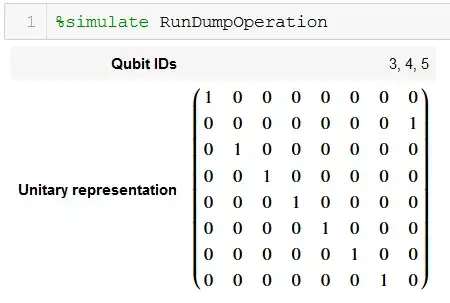
1. First observation is it has 8 rows and columns, so it is showing the table for 3 qubits.
2. Whenever it is not $|000\rangle$ and $|111\rangle$ it always add 1. $|001\rangle$ becomes $|010\rangle$ etc.
3. I ignored the complicated part just tried to implement the easy always add 1 part.
4. One observation for $|001\rangle$ to $|110\rangle$ is the LSB qubit is always flipped.
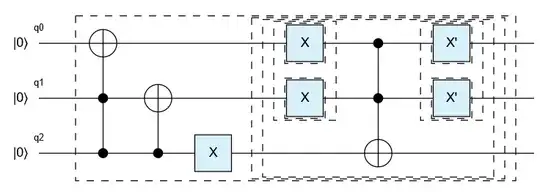
5. At this point I realized I would keep one line for $|1\rangle$ and it would help me always flip a state. (let's call it qubit 4)
6. Then I realize when would qubit 2 and qubit 1 change. Qubit 2 changes when qubit 3 and 4 both are 1. Qubit 1 change when qubit 2,3,4 are 1.

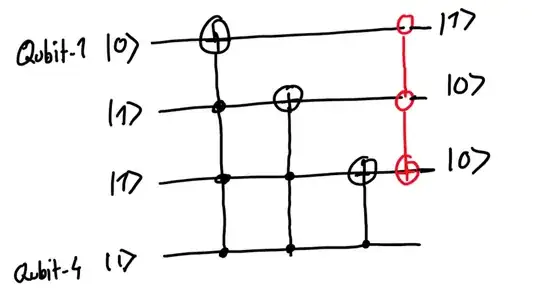
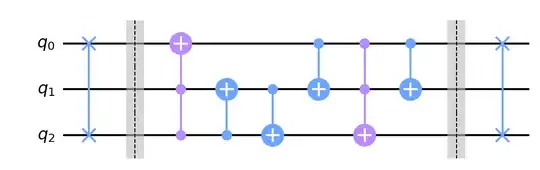
7. Then I ran the rest of the two cases and checked what output they generated and brute forced to correct it using Toffoli gates.

Is it possible to verify if this is how the puzzle is intended to be solved or did I miss something?

(Also CCCNOT gate is a feasible gate right? or am I making things up?)

Answer 1

$\newcommand{\ket}[1]{\left|{#1}\right\rangle}\newcommand{\+}{\oplus}$Let us call this matrix as $U$. Since this is a permutation matrix, for any $x,y,z\in\{0,1\}$, $U\ket{xyz}$ equals $\ket{XYZ}$ for some $X,Y,Z\in\{0,1\}$. Then, we see that the mapping $(x,y,z)\mapsto X$ is a boolean function, and can be written in terms of $x,y,z$ using AND and XOR. Similarly, $Y$ and $Z$ are boolean functions of $x,y,z$.

The matrix $U$ can be written in the standard basis as $$ \begin{align*} U\ket{000}&=\ket{000}\\ U\ket{001}&=\ket{010}\\ U\ket{010}&=\ket{011}\\ U\ket{011}&=\ket{100}\\ U\ket{100}&=\ket{101}\\ U\ket{101}&=\ket{110}\\ U\ket{110}&=\ket{111}\\ U\ket{111}&=\ket{001} \end{align*} $$ This 'table' can be written as the following boolean formula: $$ \begin{aligned} U\ket{xyz}&=(1\+x)(1\+y)(1\+z)&\ket{000}\\ &+(1\+x)(1\+y)z&\ket{010}\\ &+(1\+x)y(1\+z)&\ket{011}\\ &+(1\+x)yz&\ket{100}\\ &+x(1\+y)(1\+z)&\ket{101}\\ &+x(1\+y)z&\ket{110}\\ &+xy(1\+z)&\ket{111}\\ &+xyz&\ket{001} \end{aligned} $$ For example, $U\ket{011}=\ket{100}$, and $\ket{xyz}=\ket{011}$ iff $(1\+x)yz=1$, so we have the term $(1\+x)yz\ket{100}$ in the above equation.

Now, we can compute $X, Y, Z$ in terms of $x,y,z$: for example, $X=1$ for $\ket{100},\ket{101},\ket{110},\ket{111}$, and the amplitudes for these are $(1\+x)yz$, $x(1\+y)(1\+z)$, $x(1\+y)z$, $xy(1\+z)$. Since they must be all exclusive ($U$ is permutation), we can XOR them together: $$ \begin{aligned} X&=(1\+x)yz\+x(1\+y)(1\+z)\+x(1\+y)z\+xy(1\+z)\\ &=yz\+xyz\+x\+xy\+xz\+xyz\+xz\+xyz\+xy\+xyz\\ &=x\+yz. \end{aligned} $$ Similarly we can compute $Y, Z$, and get $Y=y\+z$, $Z=x\+y\+xy\+yz\+zx$.

Hence, $U\ket{xyz}=\ket{x\+yz}\ket{y\+z}\ket{x\+y\+xy\+yz\+zx}$.

In our attempt to implement $U$, we can see that at least implementing $x\+yz$ and $y\+z$ is easy:

So the problem is: given $a=x\+yz$, $b=y\+z$, $c=z$, implement $x\+y\+xy\+yz\+zx$.

Then, we have $z=c$, $y=b\+c$, $x=a\+yz=a\+(b\+c)c$. So,

$$x\+y\+xy\+yz\+zx=c\+a\+b\+ab$$

But this is easy to implement:

Combining the two circuits, we obtain

Answer 2

Looking at the book, I'm not sure whether the exercise allows to allocate extra qubits in the $|1\rangle$ state to enable implementing the X gate using the CNOT gate (if the allocated qubits start in the $|0\rangle$ state, you'd need an X gate to flip them to $|1\rangle$ to use them as controls, which seems a chicken-and-egg problem). If not, the last gate in the circuit can be problematic, since it's controlled on zero state of the qubits, and requires X gates to implement it from the Toffoli gate.

If X gates are fair game (on their own or using an extra $|1\rangle$ qubit), this would work.

Here's a trick I used to validate this (applying the gates to 8 basis states separately by hand seems like a lot of work and can be error-prone): implement the circuit in Q# and use DumpOperation to print its matrix.

open Microsoft.Quantum.Arrays;
open Microsoft.Quantum.Diagnostics;
operation PartialPermutation (qs : Qubit[]) : Unit is Adj+Ctl {
    // reverse the order of qubits to get matrix with big endian indices
    let qsBE = Reversed(qs);
    Controlled X(qsBE[1 .. 2], qsBE[0]);
    Controlled X([qsBE[2]], qsBE[1]);
    X(qsBE[2]);
    ControlledOnInt(0, X)(qsBE[0 .. 1], qsBE[2]);
}
operation RunDumpOperation () : Unit {
    DumpOperation(3, PartialPermutation);
}

Update: the circuit implemented by the operation (without qubit order reversal, so that it looks more like the circuit in the question):

Answer 3

I think... I just guessed a circuit.

This figure is generated by Qiskit. Only circuits between the gray dashed barriers are relevant! This is due to the different conventions of Qiskit's and Nielsen and Chuang's multi-qubit state-vector. Qiskit's convention is $|q_2 q_1 q_0\rangle$, while Nielsen and Chuang's is $|q_0 q_1 q_2\rangle$. That's the reason for adding those two swap gates.

That was really guessed! (T.T) Currently, I have no references for this result.

---

To generate this circuit, the following Qiskit code could be utilized:

import numpy as np
from qiskit import QuantumCircuit
from qiskit.quantum_info import Operator
circ1 = QuantumCircuit(3)
circ1.swap(0, 2)
circ1.barrier()
circ1.toffoli(1, 2, 0)
circ1.cnot(2, 1)
circ1.cnot(1, 2)
circ1.cnot(0, 1)
circ1.toffoli(0, 1, 2)
circ1.cnot(0, 1)
circ1.barrier()
circ1.swap(0, 2)
circ1.draw()

The Matrix representation of this circuit is then

>>> np.array(Operator(circ1).data, dtype=int)
array([[1, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 1],
       [0, 1, 0, 0, 0, 0, 0, 0],
       [0, 0, 1, 0, 0, 0, 0, 0],
       [0, 0, 0, 1, 0, 0, 0, 0],
       [0, 0, 0, 0, 1, 0, 0, 0],
       [0, 0, 0, 0, 0, 1, 0, 0],
       [0, 0, 0, 0, 0, 0, 1, 0]])

---

The answer from Mariia Mykhailova, and also the question itself, are substantially clearer and easy to comprehensive to me. The circuit could also be verified:

circ2 = QuantumCircuit(3)
circ2.swap(0, 2)
circ2.barrier()
circ2.toffoli(1, 2, 0)
circ2.cnot(2, 1)
circ2.x(0); circ2.x(1); circ2.x(2)
circ2.toffoli(0, 1, 2)
circ2.x(0); circ2.x(1)
circ2.barrier()
circ2.swap(0, 2)
circ2.draw()

>>> np.allclose(Operator(circ1), Operator(circ2))
True

So the circuit below should be exactly the same compared to the circuit above.