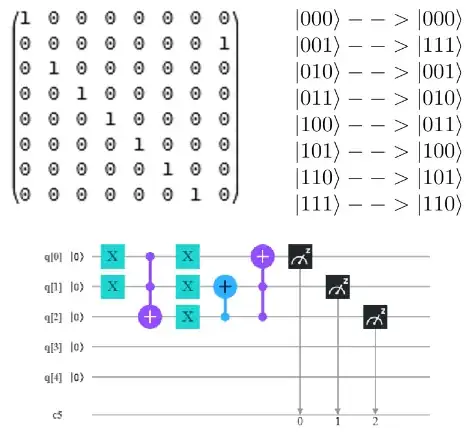
First, your transformation is not correct. Imagine multiplying this matrix with $|1\rangle$, and the result would be $|2\rangle$ instead of $|7\rangle$.
Personally, I prefer the method provided in this slide. I do not understand Japanese, but hopefully, I have gotten its general idea. Next, I will explain that idea with a detailed circuit drawing.
The circuit $U$ transforms the computational basis
$$|0\rangle\rightarrow|0\rangle\quad|1\rangle\rightarrow|2\rangle\quad|2\rangle\rightarrow|3\rangle\quad|3\rangle\rightarrow|4\rangle\quad|4\rangle\rightarrow|5\rangle\quad|5\rangle\rightarrow|6\rangle\quad|6\rangle\rightarrow|7\rangle\quad|7\rangle\rightarrow|1\rangle$$
Let $P_{mn}$ represent $|m\rangle\leftrightarrow|n\rangle$. Then,
$$U=P_{12}P_{23}P_{34}P_{45}P_{56}P_{67}$$
We can implement each one based on their binary representation. Note that Toffoli=$P_{67}$, and the Fredkin gate in Exercise 4.25 is $P_{56}$. Most $P$ here can be implemented similarly with either Toffoli or Fredkin.
$P_{34}$ is tricky, though. Nevertheless, we can replace it with $P_{35}P_{45}P_{35}$. To see that, we can verify with $|3\rangle\rightarrow|5\rangle\rightarrow|4\rangle\rightarrow|4\rangle$, $|4\rangle\rightarrow|4\rangle\rightarrow|5\rangle\rightarrow|3\rangle$, and $|5\rangle\rightarrow|4\rangle\rightarrow|3\rangle\rightarrow|5\rangle$.
The final circuit is
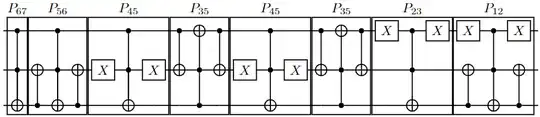
Although there are simpler circuits for this question, this idea is nice because it is general in some sense. Some theory probably says that any permutation can be decomposed into pair-wise permutations $P_{mn}$. So, maybe this method can also solve some other permutation problems.