How do you represent one-qubit rotations in two registers as a $4\times 4$ unitary matrix?

Question

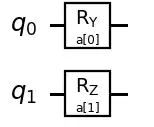
Let's say you have a circuit that performs a Z-rotation in the first register, and a Y-rotation in second register. How can we express this "moment" in terms of a 4x4 matrix, i.e. a two-qubit gate? My end goal is to express the circuit below in terms of only tfq.util.get_supported_gates :

{cirq.X: 1,
 cirq.XX: 2,
 cirq.Y: 1,
 cirq.YY: 2,
 cirq.Z: 1,
 cirq.ZZ: 2,
 cirq.H: 1,
 cirq.CZ: 2,
 cirq.CNOT: 2,
 cirq.SWAP: 2,
 cirq.ISWAP: 2,
 cirq.FSimGate(theta=0.123, phi=0.456): 2,
 cirq.I: 1,
 cirq.PhasedXPowGate(phase_exponent=0.123): 1,
 cirq.PhasedISwapPowGate(phase_exponent=0.123): 2}

But I would like to start by understanding how I would represent just the first stacked Y- and Z-rotation in terms of a 4x4 matrix. For each moment, after I have the matrix representation, I plan to use cirq.two_qubit_matrix_to_operations to decompose this quasi-two-qubit operation into Z/XY/CZ gates.

Are either of these the correct representation for $Rz(\gamma)$ and $Ry(\theta)$ rotations in registers one and two respectively?

1. $$ \begin{pmatrix} \cos{\theta} & -\sin{\theta} & 0 & 0 \\ \sin{\theta} & \cos{\theta} & 0 & 0 \\ 0 & 0 & e^{-i\gamma/2} & 0 \\ 0 & 0 & 0 & e^{i\gamma/2} \end{pmatrix} $$

2. $$ \begin{pmatrix} e^{-i\gamma/2}\cos{\theta} & 0 & -e^{-i\gamma/2}\sin{\theta} & 0 \\ 0 & e^{i\gamma/2}\cos{\theta} & 0 & -e^{i\gamma/2}\sin{\theta} \\ e^{-i\gamma/2}\sin{\theta} & 0 & e^{-i\gamma/2}\cos{\theta} & 0 \\ 0 & e^{i\gamma/2}\sin{\theta} & 0 & e^{i\gamma/2}\cos{\theta} \end{pmatrix} $$

KAJ226 · Accepted Answer · 2020-12-20T03:30:45.193

Note 100% sure if this is what you are asking but when you have a circuit like:

and you want to write it as a $4 \times 4$ Unitary matrix $U$ then you can do it as:

$ U = R_y(a[0]) \otimes R_z(a[1]) $

This can be generalized to any size as well. So if you have

then it can be written as an $8 \times 8$ matrix $U$ as $U = R_y(a[0]) \otimes R_z(a[1]) \otimes H $.

Note that if $ A = \begin{pmatrix} a_1 & a_2 \\ a_3 & a_4 \end{pmatrix}$ and $ B = \begin{pmatrix} b_1 & b_2 \\ b_3 & b_4 \end{pmatrix}$ then $A \otimes B = \begin{pmatrix} a_1 \cdot B & a_2 \cdot B\\ a_3 \cdot B & a_4 \cdot B \end{pmatrix} $

Update: So to be explicit, we can see that:

\begin{align} R_y(2\theta_1) \otimes R_z(2 \theta_2) &= \begin{pmatrix} \cos\theta_1 & -\sin\theta_1 \\ \sin\theta_1 & \cos\theta_1 \end{pmatrix} \otimes \begin{pmatrix} e^{-i \theta_2} & 0 \\ 0 & e^{i \theta_2} \end{pmatrix}\\ &= \begin{pmatrix} \cos\theta_1 \begin{pmatrix} e^{-i \theta_2} & 0 \\ 0 & e^{i \theta_2} \end{pmatrix} & -\sin \theta_1 \begin{pmatrix} e^{-i \theta_2} & 0 \\ 0 & e^{i \theta_2} \end{pmatrix} \\ \sin \theta_1 \begin{pmatrix} e^{-i \theta_2} & 0 \\ 0 & e^{i \theta_2} \end{pmatrix} & \cos \theta_1 \begin{pmatrix} e^{-i \theta_2} & 0 \\ 0 & e^{i \theta_2} \end{pmatrix} \end{pmatrix}\\ &= \begin{pmatrix} \cos\theta_1 e^{-i \theta_2} & 0 & -\sin \theta_1 e^{-i \theta_2} & 0\\ 0 & \cos \theta_1 e^{i \theta_2} & 0 & -\sin\theta_1 e^{i\theta_2}\\ \sin\theta_1 e^{-i \theta_2} & 0 & \cos \theta_1 e^{-i \theta_2} & 0\\ 0 & \sin \theta_1 e^{i \theta_2} & 0 & \cos\theta_1 e^{i\theta_2}\\ \end{pmatrix} \end{align}

And if you don't want to do this by hand in the future, then you can do this operation pretty fast in python:

import numpy as np 
import sympy as sym
x1 = sym.Symbol('x1')
x2 = sym.Symbol('x2')
i = sym.Symbol('i')
Ry = [[sym.cos(x1), -sym.sin(x1)], [sym.sin(x1),sym.cos(x1)]] 
Rz = [[sym.exp(-i*x2),0], [0,sym.exp(i*x2)]]
U = np.kron(Ry,Rz)
print(U)

score 3 · Answer 2 · answered Dec 21 '20 at 19:19

The easiest way to get the unitary matrix of a couple of operations in Cirq is the unitary method on the Circuit class. In your case:

import cirq
a, b = cirq.LineQubit.range(2)
theta = 0.4
phi = 0.123
u = cirq.Circuit(cirq.rx(phi)(a), cirq.rz(theta)(b)).unitary()
print(u)

Will give you the 4x4 unitary matrix

[[ 0.97821373-0.19829374j  0.        +0.j         -0.01221046-0.06023611j   0.        +0.j        ]
 [ 0.        +0.j          0.97821373+0.19829374j  0.        +0.j   0.01221046-0.06023611j]
 [-0.01221046-0.06023611j  0.        +0.j          0.97821373-0.19829374j   0.        +0.j        ]
 [ 0.        +0.j          0.01221046-0.06023611j  0.        +0.j   0.97821373+0.19829374j]]

How do you represent one-qubit rotations in two registers as a $4\times 4$ unitary matrix?

2 Answers2