Hadamard Test to calculate imaginary part

Question

I am trying to understand the Hadamard Test by finding the average value of $U_1$, which is a diagonal matrix with $1$ everywhere except on the first element.

I performed the regular Hadamard Test as presented in the wiki page:

and so far so good, everything works as it should.

What is the circuit variant to perform the Hadamard Test to calculate the imaginary part? The wiki page says you only have to start with $\frac{1}{\sqrt{2}}(|0\rangle-i |1\rangle)$ instead of $H|0\rangle$, I attempted doing the test adding a phase shift of -i on $|0\rangle$ by applying $U_s$ = $\begin{bmatrix}\ 1 & 0 \\ 0 & -i \end{bmatrix}$ on the control qubit after $H$, but all im getting is random measurements

Answer 1

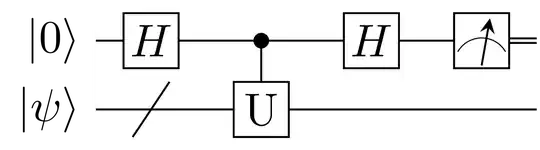
Here is a circuit for calcualating $Im(\langle\psi|U |\psi \rangle)$ (circuit composer from IBM):

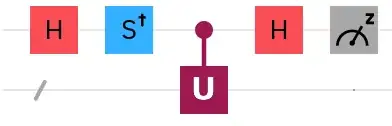
Initial state: $$|\Psi_0 \rangle=|0\rangle |\psi\rangle$$

After $S^{\dagger} H$ on the first qubit:

$$|\Psi_1 \rangle=\frac{1}{\sqrt{2}}(|0\rangle - i|1\rangle) |\psi\rangle$$

Controlled $U$

$$|\Psi_2 \rangle=\frac{1}{\sqrt{2}}(|0\rangle |\psi\rangle - i|1\rangle U |\psi\rangle)$$

After final Hadamard on the control qubit:

\begin{align*} |\Psi_3 \rangle &=\frac{1}{2} \big[(|0\rangle + |1\rangle) |\psi\rangle - i(|0\rangle - |1\rangle) U |\psi\rangle \big] = \\ &=\frac{1}{2} \big[|0\rangle (|\psi\rangle - i U |\psi\rangle) + |1\rangle(|\psi\rangle + i U |\psi\rangle) \big] \end{align*}

The probability of measuring $|0\rangle$ and the probability of measuring $|1\rangle$:

$$p_0 = \frac{1}{4}\big[(\langle \psi | + i \langle \psi | U^{\dagger})(|\psi\rangle - i U |\psi\rangle) \big]= \frac{1}{4}\big[2 - i \langle\psi|U|\psi\rangle + i \langle\psi|U^{\dagger}|\psi\rangle \big] \\ p_1 = \frac{1}{4}\big[(\langle \psi | - i \langle \psi | U^{\dagger})(|\psi\rangle + i U |\psi\rangle) \big]= \frac{1}{4}\big[2 + i \langle\psi|U|\psi\rangle - i \langle\psi|U^{\dagger}|\psi\rangle \big]$$

because $U^\dagger U = I$ and $\langle \psi|\psi \rangle = 1$. Calculating the expectation value of $\sigma_z$:

$$\langle \sigma_z \rangle = p_0 - p_1 = -i \frac{\langle\psi|U |\psi \rangle - \langle\psi| U^{\dagger} |\psi \rangle}{2} = Im(\langle\psi|U |\psi \rangle)$$

So the circuit works as was described in the Wikipedia page about the Hadamard test.

Answer 2

Here, I think you wanted this link

OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[1];
x q[0];
x q[1];
h q[0];
s q[0];
cu1(pi) q[0],q[1];
h q[0];
measure q[0] -> c[0];