2

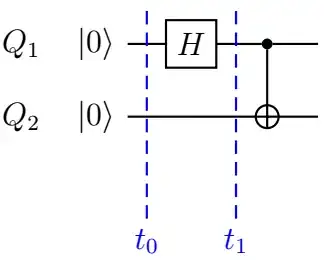
I understand that starting with

Entanglement circuit,

we can get to $\vert \Phi^+ \rangle$. First, we start with $\vert Q_1 \rangle \otimes \vert Q_2 \rangle = \vert 0 \rangle \otimes \vert 0 \rangle$ and then applying $H$ on $Q_1$ which gives $\left( \frac{1}{\sqrt{2}}\vert 0 \rangle + \frac{1}{\sqrt{2}}\vert 1 \rangle \right)\otimes \vert 0 \rangle$. After $t_1$, we obtain $\frac{1}{\sqrt{2}}\vert 00 \rangle + \frac{1}{\sqrt{2}}\vert 10 \rangle$. Then, we apply the $CNOT$ gate to end up with $$\vert \Phi^+ \rangle = \frac{1}{\sqrt{2}}\vert 00 \rangle + \frac{1}{\sqrt{2}}\vert 11 \rangle.$$

I am wondering if there is a way to show all of this using the matrix representation of gates. I have tried the following way but I can't seem to get it properly:

We start with the state $\vert 00 \rangle = \scriptstyle\begin{bmatrix}1\\0\\0\\0\end{bmatrix}$. Between $t_0$ and $t_1$, I applied $$H \otimes I = \begin{bmatrix}\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 & 0\\\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & 0\\ 0 & 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\0 & 0 & \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}\end{bmatrix},$$ since we are manipulating $Q_1$ and leaving $Q_2$ unchanged to obtain $\scriptstyle\begin{bmatrix}\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\\0\\0\end{bmatrix}$. Lastly, we apply $CNOT$ which gives us $\scriptstyle\begin{bmatrix}\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\\0\\0\end{bmatrix}.$

I am really looking for the matrices required to achieve the desired result.

glS
  • 27,510
  • 7
  • 37
  • 125
M. Al Jumaily
  • 824
  • 1
  • 6
  • 19

2 Answers2

6

I think the problem of the calculations is in the $H \otimes I$, that should be equal to:

\begin{equation} H \otimes I = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \cdot I & 1 \cdot I \\ 1 \cdot I & -1 \cdot I \end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1\\ 1 & 0 &-1 & 0\\ 0 & 1 & 0 &-1 \end{pmatrix} \end{equation}

Then if we will apply this to $|00\rangle$ state we will obtain:

\begin{equation} H \otimes I |00\rangle= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1\\ 1 & 0 &-1 & 0\\ 0 & 1 & 0 &-1 \end{pmatrix} \begin{pmatrix} 1\\0\\0\\0 \end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1\\0\\1\\0 \end{pmatrix} \end{equation}

Now let's apply the CNOT gate:

\begin{equation} CNOT \frac{1}{\sqrt{2}}\big(|00\rangle + |10\rangle\big)= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} 1\\0\\1\\0 \end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1\\0\\0\\1 \end{pmatrix} = \frac{1}{\sqrt{2}}\big(|00\rangle + |11\rangle\big) \end{equation}

Davit Khachatryan
  • 4,461
  • 1
  • 11
  • 22
0

I think you're looking for

$$B \space = \space CNOT \space \space (H \otimes I) = \begin{bmatrix}1&0&1&0\\0&1&0&1\\0&1&0&-1\\1&0&-1&0\end{bmatrix}\frac{1}{\sqrt{2}}$$

or an equivalent permutation

$$B = ( X \otimes X + Z \otimes I ) \frac{1}{\sqrt{2}} = \begin{bmatrix}1&0&0&1\\0&1&1&0\\0&1&-1&0\\1&0&0&-1\end{bmatrix}\frac{1}{\sqrt{2}}$$

in which the four columns are the Bell's states:

$$B\left |00\right> = \left |\Phi^+\right>$$

$$B\left |01\right> = \left |\Psi^+\right>$$

$$B\left |10\right> = \left |\Psi^-\right>$$

$$B\left |11\right> = \left |\Phi^-\right>$$

I showed something similar in another answer about Bell's states preparation.

Matteo Vitturi
  • 171
  • 6