The answers given so far make many good points. One problem with the question is that it's implicitly simplifying the context. So I'd like to give a more detailed answer, which is a qualified "yes". Curvature is "affected" not only by energy-mass, but also by momentum – which is related to velocity – and also by energy & momentum fluxes, like heat and pressure (see the pedagogical article by Ehlers & al. below).
First let's be more precise on a couple of points:
"Curvature", in its most general form important for general relativity, is not something which can be quantified by one number. It is expressed by a set of numbers, called a tensor, and their values depend on the coordinate system which we adopt in a region of spacetime. Simplifying things a little, your "curvature in the $x$-direction" could be a combination of my "curvatures in the $x'$ and $y'$ directions", if we're using two different coordinate systems $(t,x,y,z)$ and $(t',x',y',z')$.
One particular set of curvature numbers, called the Einstein tensor, can be represented by a 4-by-4 symmetric matrix of numbers $G^{\mu\nu}$. This matrix can also be represented by an ellipsoid (or hyperboloid) in spacetime. This is the curvature tensor that enters directly in the Einstein equations.
If at a spacetime point where there's a non-zero amount of matter, by which we mean some substance, or baryons or leptons, then we can associate to that matter at that point a four-velocity vector $U^{\mu}$. This is also a collection of four numbers, which again depend on the coordinate system. If we are using one temporal and three spatial coordinates $(t,x,y,z)$, then the spatial components of the four-velocity $(U^x, U^y, U^z)$ are proportional to the coordinate velocities. Clearly we can choose a coordinate system in which the coordinate velocities are zero (at least in a small region).
We represent the energy and momentum (their densities and fluxes) of matter by an energy-momentum tensor, which can be represented by a 4-by-4 matrix $T^{\mu\nu}$ of numbers, again dependent on the coordinates. In the simple case of matter whose internal pressure is negligible, called "dust", its energy-momentum tensor is directly given in terms of its four-velocity:
$$T^{\mu\nu} = \rho\,U^{\mu}\,U^{\nu}$$
where $\rho$ is the rest-energy density.
Now we can say this unambiguously: four-velocity "affects" curvature. In fact this comes directly from the Einstein equations:
$$G^{\mu\nu} = \kappa T^{\mu\nu}$$
where $\kappa$ is a proportionality constant. In the case of "dust" matter we have
$$
G^{\mu\nu} = \kappa \rho \,U^{\mu}\,U^{\nu}
$$
which clearly says, for instance, that the curvature $G^{xy}$ is proportional to the $x$ and $y$ coordinate velocities. So yes, if the matter at a given point has a higher $x$-velocity, then it's also generating higher $G^{x\nu}$ curvatures there.
This will also be reflected in the metric tensor, which will contain off-diagonal terms proportional to $\rho U^x$, and called "gravitational vector potential". In a first approximation they are somewhat analogous to the magnetic field, but for gravitation. Indeed the curvature effects coming from velocity are called "gravitomagnetic effects". These effects are concretely considered by the International Astronomical Union in their modelling of the solar system; see references below.
[For the sake of correctness, the fact that the four-velocity (and hence the coordinate velocities) affect Einstein curvature is not a pure consequence of the Einstein equations, but a consequence of them together with the fact that the energy-momentum tensor of matter depends on the four-velocity. One can also create models of matter whose energy-momentum tensor does not depend on the four-velocity, for instance $T^{\mu\nu}=\lambda g^{\mu\nu}$, where $g^{\mu\nu}$ is the inverse metric tensor. Such matter would correspond to a cosmological constant; see the pedagogical article by Ehlers & al.]
But it's important to emphasize the coordinate-dependence of velocity components, curvature components, and their interpretation. A picture may help. Consider a point in spacetime where we have matter with four-velocity $U^{\mu}$ and Einstein curvature $G^{\mu\nu}$, related by the equation above. We can visualize them as follows:
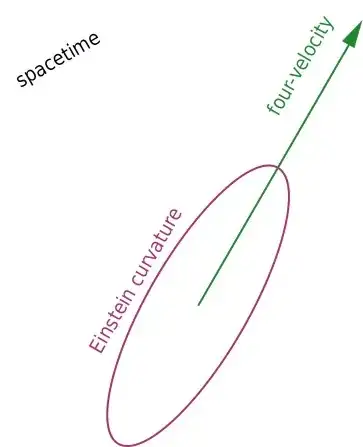
Note that this is not a spacetime-diagram. It's just a (quite faithful) illustration of the four-velocity and of the Einstein tensor in two dimensions. Also, we are considering matter that does have internal pressure. There is a relation between four-velocity and Einstein curvature because if the four-velocity vector were longer, then the ellipse would have a longer major axis as well.
Now we can introduce a coordinate system $(t,x)$ as follows (the axes looks orthogonal, but that's unimportant):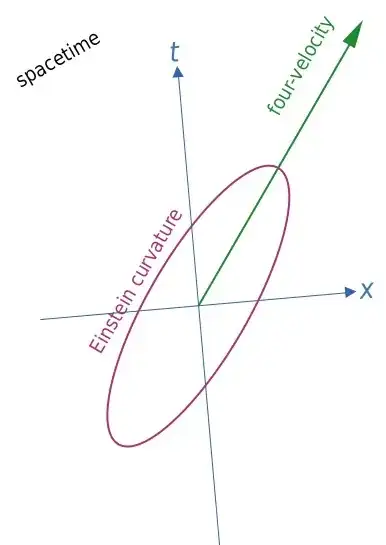
In these coordinates, the matter at this spacetime point has non-zero coordinate $x$-velocity, and the Einstein curvature has a particular $G^{xx}$ component, represented by the intersection between the ellipse and the $x$-axis. This value is proportional to the square of the $x$-velocity and to the pressure. Note how the ellipse is skew with respect to this coordinate system. We interpret this skewness as being an effect of the non-zero velocity with respect to this coordinate system.
But we can also introduce a different coordinate system $(t',x')$ as follows: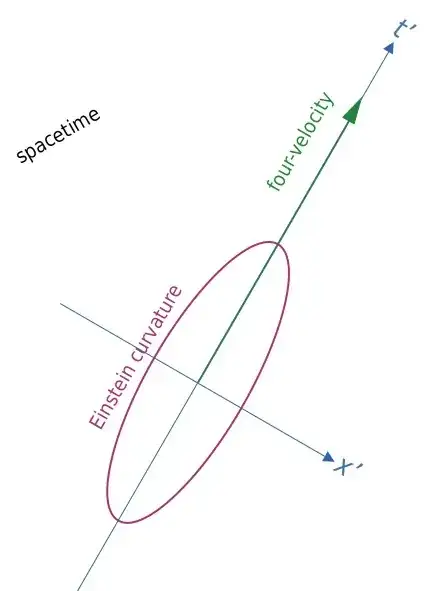
In these coordinates, the matter is at rest, with zero $x'$-velocity. The Einstein curvature has a particular $G^{x'x'}$ component, proportional to the pressure. Note how the ellipse is now not skewed with respect to this coordinate system. We interpret this absence of skewness as being an effect of the zero velocity with respect to this coordinate system.
Clearly the physical situation is the same.
References
For the representation of symmetric matrices as ellipses:
On gravitomagnetism there is introductory material in many places; for instance:
Gravitomagnetism in the International Astronomical Union specifications for coordinate systems for solar system and Earth:
On the cosmological constant, interpreted as a kind of matter:


