Why is current a scalar quantity?

Question

Current has both magnitude and direction. As per the definition of vector defined in encyclopedia, current should be a vector quantity. But, we know that current is a scalar quantity. What is the reason behind it?

Answer 1

To be precise, current is not a vector quantity. Although current has a specific direction and magnitude, it does not obey the law of vector addition. Let me show you.

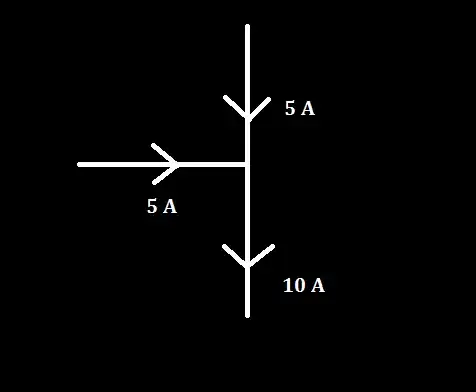
Take a look at the above picture. According to Kirchhoff's current law, the sum of the currents entering the junction should be equal to sum of the currents leaving the junction (no charge accumulation and discharges). So, a current of 10 A leaves the junction.

Now take a look at the picture below.

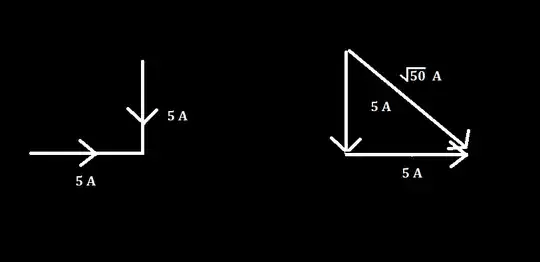
Here, I have considered current to be a vector quantity. The resultant current is less than that obtained in the previous situation. This result gives us a few implications and I would like to go through some of them. This could take place due to charge accumulation at some parts of the conductor. This could also take place due to charge leakage. In our daily routine, we use materials that are approximately ideal and so these phenomena can be neglected. In this case, the difference in the situations is distinguishable and we cannot neglect it.

If you are not convinced, let me tell you more. In the above description (current as a vector), I have talked about the difference in magnitudes alone. The direction of the resultant current (as shown) is subtle. That's because in practical reality, we do not observe the current flowing along the direction shown above. You may argue that in the presence of the conductor, the electrons are restricted to move along the inside and hence it follows the available path. You may also argue that the electric field inside the conductor will impose a few restrictions. I appreciate the try but what if I remove the conductors? And I also incorporate particle accelerators that say shoot out proton beams thereby, neglecting the presence of an electric field in space.

Let me now consider two proton beams (currents), each carrying a current of 5 A as shown below. These beams are isolated and we shall not include any external influences.

Now that there is no restriction to the flow of protons, the protons meeting at the junction will exchange momentum and this will result in scattering (protons represented by small circles). You would have a situation where two beams give rise to several beams as shown below. Our vector addition law does not say this.

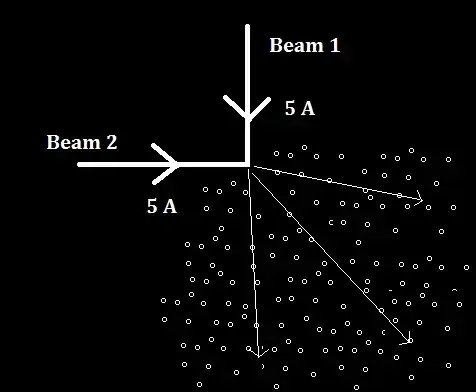
I have represented a few in the picture above. In reality, one will observe a chaotic motion. Representation of the beams (as shown right above) will become a very difficult task because the protons do not follow a fixed path. I have just shown you an unlikely, but a possible situation.

All this clearly tells us that current is not a vector quantity.

Another point I would like to mention is, current cannot be resolved into components unlike other vector quantities. Current flowing in a particular direction will always have an effect along the direction of flow alone over an infinite period of time (excluding external influences such as electric or magnetic fields).

Answer 2

I think there might be a contextual issue.

If you're passing DC current in a circuit, it makes sense to treat it as a scalar, because it flows along the wires and you're usually designing the circuit so that its components don't appreciably interact in ways where the wire geometry matters... or rather treating ones that do as separate sub-units, e.g., inductors.

In other words, if your current is constrained to go in one dimension, such as along wires, then it makes sense for it to be treated as a scalar, because a $1$-dimensional vector is a scalar.

But as the case of inductors shows, the direction in space the current is flowing can make a lot of difference electromagnetically. As BMS suggested, more fundamentally the conservation of charge is expressed by a continuity equation $$\frac{\partial\rho}{\partial t} + \nabla\cdot\mathbf{J} = 0\text{,}$$ where $\rho$ and $\mathbf{J}$ are charge and current densities, respectively, quantities that also appear in Maxwell's equations.

---

Here's some context that may make the original post clear. The force on a current-carrying wire ... $\vec{F}=I\vec{L}\times\vec{B},$ ... As another example, the Biot-Savart law is $d\vec{B}=\frac{\mu_o}{4\pi} \frac{Id\vec{l}\times\hat{r}}{r^2},$ where $d\vec{l}$ is in the same direction as the "current" $I$.

One can obviously rewrite that as $L\vec{I}\times\vec{B}$ and $dl(\vec{I}\times\vec{r})$ if one wished to think of a vector current. The only reason not to would be the fact that your amp-meter tells you directionality along a wire (hence $\pm$) rather than directionality in space, so the fact that it's more convenient the other way.

Answer 3

Current doesn't follow vector addition and decomposition law, and so it is not a vector quantity. Current density is a vector quantity.

Answer 4

I think a cleaner idea is to show that current has a sign, but it does not have a direction.

In particular, current is the amount of charge crossing a surface per unit time. This can be shown to be equal to the quantity:

$$I = \int d{\vec A} \cdot \rho {\vec v}$$

Where $d{\vec A}$ is the surface element of the surface in question, $\rho$ is the charge density of the fluid, and $\vec v$ is the flow rate of the fluid. This is obviously a scalar quantity, and now it should be clear why it's possible to have positive and negative currents -- it just depends on whether the charge is flowing to the "right" or to the "left" through the surface.

Answer 5

current is definitely a vector quantity as flow of electrons leads to formation of electric force and current also and force is a vector quantity and secondly flow of electrons in per unit time called current and flow of electrons literally means moving in a definite direction