If current is scalar quantity, why do we assume negative current in nodal analysis?

Question

The electric current intensity is scalar quantity because it's equal to

$$I=\int_{S}^{}\vec{J}\cdot\mathrm{d}\vec{S}$$

but in some circuit analysis we say there is a negative current like this :

we say that this current source is equivalent to this current source

or something like this

we say this branch is equivalent to

but how this equivalency work and the current is not a vector quantity? how do we say that it even has a direction and toggle its direction up and down and put a negative sign and it's not a vector quantity?

Answer 1

Although current has both magnitude and direction, it is a scalar quantity because if follows laws of scalar addition rather than vector addition. Consider the two circuits below. Electrically, the two circuits having identical resistors and voltage sources are identical.

In applying KCL to node A, for both diagrams we use scalar addition, i.e., the algebraic sum of the currents into the node is zero, or, considering current into the node as positive, we have, for both diagrams,

$$I_{1}-I_{2}-I_{3}=0$$

Note that this depends only on the directions of the currents insofar as whether they are directed into or out of the node. It does not depend upon the vertical and horizontal components of the current, which are different in the case of current $I_1$ in the two diagrams.

If instead of three currents we had three forces acting on point A, then vector addition would be needed to determine the requirements for equilibrium at point A, i.e., $\sum \vec F=0$. Forces are true vector quantities.

Hope this helps.

Answer 2

Look at the integral

$$I=\int_{S}^{}\vec{J}\cdot\mathrm{d}\vec{S}\tag{1}.$$

For this to make sense, the surface $S$ should be orientable, that is, it should be possible to assign in a continuous way a normal unit vector $\hat{n}$ at each point of the surface. Once one has assigned this field of normal unit vectors, the scalar product $\mathrm{d}I = \vec{J}\cdot\hat{n}\,\mathrm{d}S$ at each point can be either positive or negative, and so the integral $I$ which is the sum of all the $\mathrm{d}I$’s. However, for a given orientable surface $S$, there are two possible orientations, which can be chosen arbitrarily. Therefore, depending on the chosen orientation, $I$ can have either sign.

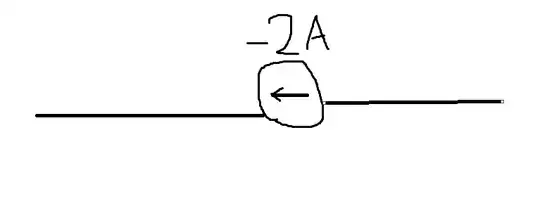
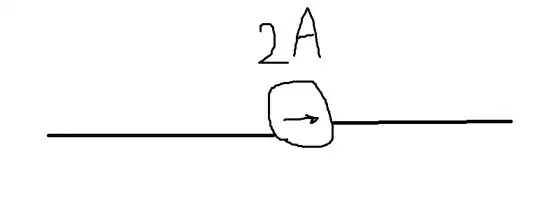
When you assign a reference direction to a wire or a component in a circuit by means of an arrow, you’re actually assigning an orientation to the surfaces crossing the wire that can be used to calculate $I$ with (1). If you reverse the reference direction, $I$ changes sign.

For instance, in the case of the first circuit with the current source, the reference direction for that source is specified by the arrow in the circle, and the minus sign on the current simply means that the integral (1), with the $\mathrm{d}S$’s oriented in agreement with the arrow, is negative. In the second circuit the arrow specifying the reference direction is reversed, and thus $I$ changes sign if the vector field $\vec{J}$ is the same.