This isn't an action from mechanics, but in gravitational lensing we look for stationary points of the time travel of light. GR basically tells us that light travels at different speeds depending on the gravitational potential. (This is distant light, not local right here in our lab.) If light from a distant quasar travels through a galaxy before reaching us, it experiences a varying gravitational potential depending on the mass distribution of the galaxy and the path the light takes. Different paths for the light then take different amounts of time. Looking in the sky, we can associate a travel time with each angle in the sky. Then we make a 2D map of travel time versus point in the sky.
Here's an example from a quick search (the source is here)
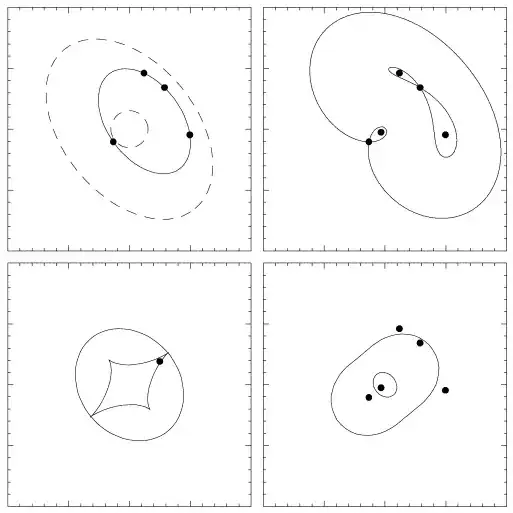
The lines connect parts of the sky that have equal travel time. The different panels show qualitatively different types of gravitational lensing systems. If you look at the upper-right panel, you see five dots, which are five distinct images of a distant quasar. The ones at intersections of contour lines are saddle points. The others are either local minima or maxima of travel time.
The difference in the time it takes light to reach Earth from different images can be dramatic - weeks or even months!
