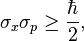Is uncertainty principle a technical difficulty in measurement?

Question

Is the uncertainty principle a technical difficulty in measurement or is it an intrinsic concept in quantum mechanics irrelevant of any measurement?

Everyone knows the thought experiment of measuring the position of an electron. One can detect electron's position by hitting it with a photon, due to Compton scattering the collision of the photon with electron will change electron's momentum. This experiment is used to explain uncertainty principle to layman, but it is over simplified, isn't it? It also gives an impression that if there was a better suited experimental method the uncertainty principle becomes irrelevant.

I personally think it is intrinsic as it arises from the non-zero commutator of position and momentum operators irrespective of the measurement process. Am I right?

EDIT: My question is similar to certain extent to this question and this question. The answers there are nice but they focus on explaining basics of quantum mechanics more than they comment on the technical difficulty part. In the answers of question 2 there are statements like "So, it's not a knowledge limit" and "you're sort of correct when you say it's an observational limit" without further comments

To summarize, assume hypothetically we managed to find a way in the future where we can have a look at an electron without disturbing it by measurement or causing its wave function to collapse, would the uncertainty principle still hold in such a case?? Why/Why not?

Answer 1

Yes, the experiment is oversimplified, because the uncertainty principle is not about "disturbance through measurement". Although that's what Heisenberg said (one of the things he said), it turned out you can't interpret it that way in a very rigorous sense.

Whether there is something like "disturbance through measurement" that gives rise to an uncertainty relation is currently under heated debate in the quantum foundations community (see the work of Ozawa and recently some collaborators on the one hand and the work of Busch, Lahti and Werner on the other, if you want, I can look up some references).

That said, your opinion is correct in the sense that this is exactly how you derive the uncertainty relation. With position and momentum, one could ask the question "but why don't position and momentum commute" and then one can turn to the Fourier transformation and remark that the uncertainty relation is something that holds for any wave (water, electromagnetic, etc.), because the Fourier transform tells us that a small wave packet must consist of a lot of frequencies and a wave with only one frequency is infinite in space, etc. Now, since we have wave functions, we have this phenomenon in quantum mechanics as well. This means that indeed the uncertainty principle in our formalism does not require any measurement, it is an intrinsic property of the wave function in phase space.

EDIT: Even with your extended question, assuming everything else would hold, the uncertainty principle should still be there. It just tells you that the product of the variances of momentum and position are lower bounded, which comes from the wave-function itself. There is no reference to any measurement in the uncertainty principle other than that you need to measure to actually compare anything.

Being more concrete, I would say the following: Given a state of an electron (i.e. a preparation scheme that prepares the exact same physical electron over and over again), you can measure momentum and you will obtain a probability distribution according to the wave function (repeating the experiment multiple times). Then, assuming you have no disturbance in measurement, you measure the position of the exact same state. In that case, this will also have some probability distribution according to the wave function. These two measured probability distributions have variances whose product is lower bounded. That's what the uncertainty principle tells you.

The question of whether or not you could have information without disturbance (at least asymptotically) is still a matter of debate...

Answer 2

My reading of the electron photon experiment is that intrinsic uncertainty enters the problem by limiting the resolving power of the photon. In other words, the electron is along for the ride, and perhaps historically it was chosen because it is such a simple system. But the recoil of the electron seems to confuse the issue.

Instead of a free electron, we can imagine scattering a photon off of a heavy nucleus or something that we consider fixed. Our goal is to use the photon to measure the position of this target. The uncertainty principle limits our ability to localize a wave packet for this purpose.

EDIT:

The uncertainty principle is fundamental. We can forego the discussion of hypothetical measurements in which we can learn the exact state of an electron without disturbing it, because we can simply prepare the electron to be in any state that we like, subject to the cleverness of experimental physicists.

So, no we have perfect knowledge of the electron's wave function. Bell's theorem tells us that we know all there is to know. Because position and momentum operators don't commute, no amount of fiddling will let us define the position and momentum of a particle simultaneously.

Just a comment about measurements that don't disturb the wavefunction: This is forbidden by the No-cloning theorem, which is rather easy to prove. However, I think weak measurement can get us arbitrarily close. Maybe someone else can elaborate. None of this effects the uncertainty principle.

Answer 3

But in practice, is there any measurement that will NOT disturb the system at all? To prove that uncertainty is beyond measurement, we must design a measurement process that does not disturb the system. If such a process cannot be designed then the statement that "uncertainty is beyond measurement" cannot be experimentally tested. Isn't it? I don't know whether the idea of a measurement with zero interaction between the system and the apparatus makes any sense, and if there is non-negligible interaction you cannot get away with disturbance induced by the process. Hence, even the theoretical arguments are logically quite robust in explaining why uncertainty principle has nothing to do with measurement, I think experimentally it is not provable (or better, not a falsifiable claim) if you don't have such an ideal measurement.

Addendum : I'm afraid to say something different. We are saying that HUP is a result of the non-commutativity of position and the corresponding momentum in the mathematical formalism of quantum mechanics. Thai is indeed correct. But having said that we have to keep in mind that the formalism of quantum mechanics was built in such a way so that its predictions match with non-classical experimental results and observations. So I personally still have a doubt and I'm not sure. After all the theory is built upon experimental observations. Correct me if I'm being foolish.

Answer 4

To summarize, assume hypothetically we managed to find a way in the future where we can have a look at an electron without disturbing it by measurement or causing its wave function to collapse, would the uncertainty principle still hold in such a case?? Why/Why not?

To start with any measurement when looked at the quantum mechanical level involves interactions, i.e. at least a photon exchange with the electromagnetic field of the particle under observation. So the thought experiment per se is not valid.

There does exist the possibility of measuring the electron's position and momentum in a non destructive way with soft photons interacting without destroying much the original momentum and position in space, within measurement errors.

And we come to the difference between measurement errors and the Heisenberg uncertainty principle. The error in measuring the momentum of the electron, in this bubble chamber photo of an electron positron pair

comes from the measurement error of the curvature in the magnetic field and the addition in quadrature of the magnetic field error . The more points fitted to the curve in the chisquare fit the smaller the curvature error. It is the measurement on one electron. The x, y,z position of the start of the electron also has corresponding measurement errors .

The Heisenberg Uncertainty Principle for this measurement tells us the following: Now that you know the momentum p_x, you cannot know the x better than

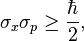
In the photo above, the HUP is fulfilled because our measurements in space cannot be better than microns and on momenta than fractions of an MeV . h_bar is a very small number and for classical sizes can be considered zero.

In this link some numbers are given on how the HUP once the momentum is known constrains the range of location in space for particles in a beam, where the numbers are small enough that the size of h_bar becomes important.

One has to keep in mind that in contrast to the nice classical curve in the photo above , the trajectory of the electron is not described by a single function. What can be described as a single function is the probability of finding an electron in a specific momentum and position, which is given by the wave function, a solution of the quantum mechanical equations.

The HUP reflects this uncertainty due to the probabilistic nature of quantum mechanics. The restrictions it imposes are useful for estimating behaviors and lifetimes etc without solving explicitly a potential problem equation and applying boundary conditions.

The HUP is the manifestation of the commutator relations which are fundamental in the structure of quantum mechanics as a theory. The uncertainty comes because the momentum and position operators do not commute. This means that the two operators cannot both display eigenvalues, i.e. accurate predictions, at the same time. This last is true for all observables from pairs of non commuting operators.