A question has recently come up that goes beyond my knowledge of special relativity. Suppose a pilot has his foot on the gas pedal of a rocket ship and keeps it applied to achieve a constant acceleration, and he has a magical engine that can maintain the thrust needed to accomplish such acceleration even as the vehicle acquires mass. He measures his acceleration at periodic intervals and sums it up as he goes.
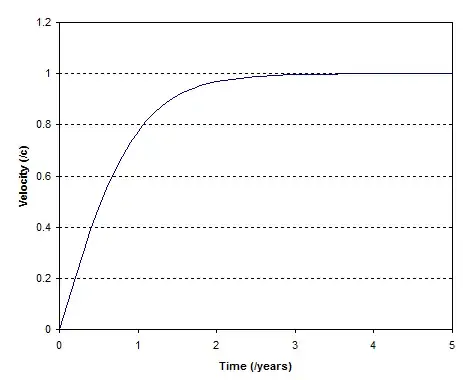
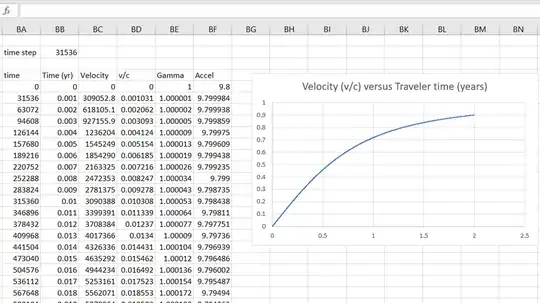
Observers perceive the rocket to increase in speed and gradually approach the speed of light (but never reach it). Two possibilities are being debated for what the pilot observes, and my preference is for the first:
- Time dilation gives him the impression that the summation of his readings are approaching light speed at a constant rate, but there is an asymptote involved here even in the inertial frame such that he never actually perceives himself to reach, let alone exceed, $c$, because time slows down to a crawl (as seen from the reference frame) before this can happen.
- Although to observers he is only approaching $c$, it is possible for the summation of the measurements on his accelerometer to indicate that he has surpassed $c$ and is now traveling faster than light. From the reference frame he is approaching $c$ and his instruments in the inertial frame tell him that he has surpassed it.
I assume (1) is true beyond a doubt? If so, is there a straightforward explanation for this?