Thanks for your interest in my answer, and I hope you found it helpful. I'll try to answer your follow-up questions as best I can below. I've re-ordered them a bit, since answering your last question helps explain some of the earlier ones.
...
I also read here: http://users.hal-pc.org/~clement/Whats%20in%20a%20Touch.pdf that electrons clouds overlap all the time, that your feet and shoes overlap the electron clouds of the atom all the time. Is this correct?
No. The article you referenced is unfortunately wrong on several key points.
Electron clouds do overlap, including across objects. Every atom contains examples of electron clouds sharing the same spaces, and sharing between atoms results in chemical bonding. Electron clouds can share the same spaces as long as they differ in some other part of a three-part "address" of space, speed, and spin. (I discuss that point in more detail later in this answer.) However, these space-sharing options get used up very quickly, both internally by individual atoms and through the formation of bonds between atoms.
So, that leaves a different question that is the right one for "touching": What happens when two electron clouds in two different atoms are pushed into each other, and there are no space-sharing options left?
The answer is that they form an extremely thin exclusion zone between them, a surface at which both electron clouds disappear. That is the exact opposite of the electron clouds overlapping. In the simplest cases, e.g. two helium atoms at bumping together at modest speeds, the resulting behaviors and shapes of the electron clouds are not all that different from those of two elastic balls getting pushed into each other, although of course the surfaces of electron clouds are a lot fuzzier. Nonetheless, like the rubber balls the two electron clouds in such cases demonstrate a definite sense of "my space" and "your space," and create a no-go zone to ensure this separation stays in place.
Electron clouds that form these no-go zones can accurately be described as the fundamental units of touching, since they retain separate locations in space, compress and deform when pushed against each other, and form a sharp, well-defined boundary or no-go zone that corresponds to their contact surface. These atomic units of touching even have much the same geometries as touching at human scales.
When you walk or run, similar no-go zones form between electron clouds on the surface of your foot and your shoe. But it doesn't stop there. The electron clouds at the surface of your foot don't like to be squeezed, so they push at the atoms behind them to try and get their original shapes back. The result is a cascade of electron clouds touching and pushing and excluding each other, until your entire foot -- your entire body actually -- is stopped cold by what began as an interaction between the atoms at the surfaces of your foot and shoe. Your foot, and you, stop at the ground instead of falling through it and landing in the center of the earth.
By the way, have you noticed how I keep saying "electron clouds" instead of "electrons"? That is intentional, because at the energy levels of chemistry you cannot see electrons as particles. The only way you can detect, change, or move them around is in the form of electron clouds -- that is, as fuzzy regions of charge and a little bit of mass that defiantly refuse to compress much below the size of an atom.
But still: Can electrons, the actual particles, ever touch each other?
No. Even with the most powerful particle accelerators ever built, electrons continue to look like infinitely small points. These points can interact in various ways, but they can never even collide directly, let alone touch. But for chemistry, worrying about electrons as particles is a bit of a red herring, an event that literally cannot happen without some outside intervention that is massively more energetic.
So, if electron clouds don't overlap when object touch, and in fact remain sharply separated instead, where did the paper you referenced go wrong?
It is a surprisingly common misunderstanding even in university chemistry programs to think that atoms are somehow held apart primarily by electrostatic repulsion. That belief can in turn lead to all sorts of misunderstandings about how and where electron clouds interact when objects collide. But touching, or the mutual exclusion of two complicated objects like feet and shoes, is a direct and unique product of the effect called Pauli exclusion, and it simply cannot be explained using electromagnetic forces alone. Pauli exclusion does not even care about electric charge, which is why the two opposite-spin electrons in a helium atom can occupy the same tiny region of space.
I alluded to Pauli exclusion earlier when I said that every electron in the universe must have its own "address" in terms of space, speed, and spin. More exactly, every electron must have seven terms in this address: three for space (x,y,z), three for speed (momentum in x,y,x), and one for spin (with only two values possible: "up" or "down"). Notice that this "turf battle" is universal: every electron in the universe must have a unique address, not just the ones you happen to be looking at.
Matter is so widely scattered in the vastness of space that the speed and spin addresses are typically less important. However, on compact little worlds like ours, all those potential address conflicts become important indeed. They are for example the reason why we don't just fall into the center of the earth. We can't go there because electrons other than the ones in our bodies have already taken up residency in the space below us, and they are not about to give of their unique addresses without a fight.
[Terry Bollinger] says:
Once the bonding has happened, however - once the atoms are in arrangements that don't leave unhappy electrons sitting around wanting to engage in close bonds - then the territorial aspect of electrons comes to the forefront: They begin defending their turf fiercely...
Does this "turf" extend past the electron? Or is it the space occupied by the electron? And what exactly are they defending it with? Is it like an electric field surrounding the electron? And is this field any less physical than the electron its self?
See the last answer for details. The electric field is irrelevant to the turf war, which depends only with the Pauli exclusion "addresses" of the electrons. Pauli exclusion is not a force at all, but a deeply quantum outcome of how the universe deals with identical objects.
The question about "what exactly are they defending [their turf] with?" is a great one, but it's also a hard one to answer without invoking mathematical terms that I don't think would provide many deeper insights at this level of description.
I can say this much: The entire universe is divided up into two types of particles, as best we can tell. One group is called fermions, and the electron is one of those. Fermions all require unique seven-part addresses just like electrons, though some of them can have more than two values for the "spin" part of that address. They are the particles we think of as "matter," that is, of things that take up space.
The other group is called bosons. You may have already guessed it: Bosons are completely fine with sharing identical space, speed, and spin addresses, and in fact they like to do it under the correct circumstances. Have you ever used a lens to focus light from the sun or a bright light? That is bosons at work: Photons or particles of light are bosons, so they don't mind getting focused onto the same spot. Bosons are deeply linked to the way forces work, with photons for example being deeply linked to how the electromagnetic force works.
Those are just descriptions, I know. Even though the mathematics of fermions and bosons are precise and highly predictive, as great a physicists as Richard Feynman never considered himself to have "gotten" why fermions really behave the way they do, at least not at a level that satisfied him. For example, it turns out that spin alone can be used to determine whether a particle is a fermion or a boson. But why? Feynman tried to answer over a period of at least 20 years, yet never really came up with an answer that satisfied him.
Another question is when he stated that they move close enough to not join but to still make "contact" how close is close enough? Is it like two balls coming together and, instead of passing through each other, elastically deform? Is it this deforming, as opposed to merging, what is referred to a repelling?
When space-sharing options have been exhausted, two electron cloud will form an exclusion zone between them no matter how far apart they are. You don't notice such things for a simple reason: Electrons clouds stick very close to their associated atomic nuclei, so they quickly fall off to very close to zero in density only a few atomic diameters away from their atoms. In that case, the exclusion zone between them becomes like zero multiplied by zero. As the atoms get within a few diameters of each other, however, you can start devising experiments that would show how they repel each other even at those relatively large distances.
If the electrons themselves don't "repel" (in the sense I outlined above), then is it some sort of field or force that repels? Is this field or force the electron cloud? If not, is this field or force present in the atom at all times? And by this logic, can this be thought off as the outer layer of the atom?
Hopefully the earlier answer about Pauli exclusion answer this one. It's not the electrical force, most definitely. The electron cloud in contrast most certainly does provide a well-defined "outer layer" of the atoms when they bump. Just be sure to discard that incorrect part about those layers overlapping. For non-sharing electron clouds, they don't, and in fact do the opposite by forming a distinct no-go zone between them.
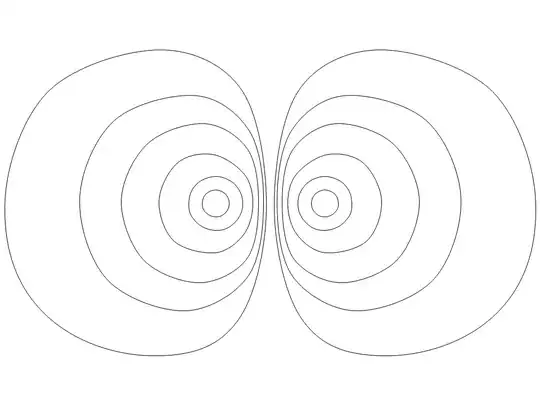
2013-11-18 - Diagram showing a two-electron-cloud exclusion zone
This figure is in response to the questions from user33996. The lines show cross sections of the surfaces for which the electron cloud density is equal, with the smaller inner loops showing higher densities. Close to the atomic centers (e.g. He$^{++}$) of the clouds these same-density surfaces become almost spherical. Near the plane of separation between the two atoms these equal-density surfaces begin to flatten out smoothly and become more plane-like in that region: