Hydrogen orbitals from non-conventional coordinate systems (Schrödinger equation)

Question

Summary: The hydrogen atom has a single electron distribution, regardless of which coordinate system is used to solve the Schrödinger equation. Note that the author is plotting the wavefunction after conversion to Cartesian system. A wave function expressed in any coordinate system should yield the same probability density for finding the electron around the nucleus. Why, then, would one accept different probability densities for orbitals obtained in different coordinate systems?

This question is related to a recent open access article (Orbitals in General Chemistry: Mathematical Realities). The authors show that the common atomic orbital shapes taught in textbooks, like a sphere for s, dumb bell shape for p orbitals, and various clover shape for the d orbitals result from solving the Schrödinger Equation in spherical coordinates.

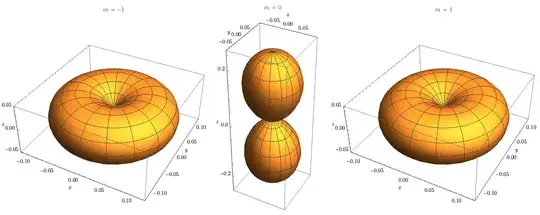
Lamoureux and Ogilvie then go on to discuss that exactly the same hydrogen-atom time independent Schrödinger equation can be solved in four alternative separations in paraboloidal, prolate spheroidal (ellipsoidal), and spheroconical coordinates—each yielding its own complete set of closed-form amplitude functions (“orbitals”) with distinct quantum-number labels.

Despite their very different shapes and quantum-number schemes (I show two examples below), all of these functions should describe identical physical states, demonstrating that orbitals are really just coordinate-dependent basis functions rather than uniquely real physical entities. This multiplicity calls into question the physical meaning the scientists ascribe to any particular orbital representation.

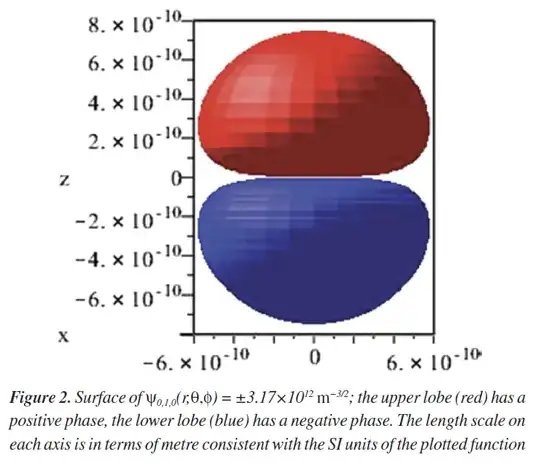
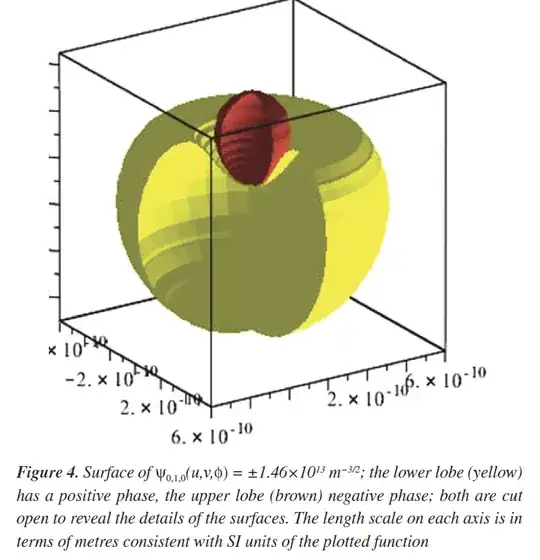
Question: Now nature does not change the reality based on the human's invention of coordinate system and hydrogen atom is unaware of the choice coordinate system. If these various coordinate‐system “orbitals” are just different basis functions for the same physical eigenstates, how do we reconcile their radically different individual shapes with the fact that the underlying probability density of the electron in the H-atom $|\Psi|^2$ must be the same? In particular, how would we demonstrate (analytically or numerically) that $|\Psi_{0,1,0}|^2$ computed in any of these coordinate systems yields the identical 3D electron‐density distribution? The figure will show the different shape in different coordinate systems.

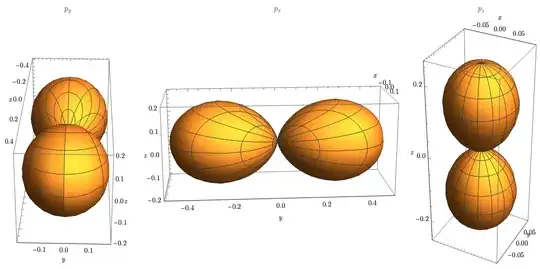
For example, most readers can recall the p-orbital shape from spherical coordinates.

however, the orbital from paraboloidal coordinate system, we get this shape from the same paper linked above.

Answer 1

tldr: The standard $\psi_{nlm}$ hydrogen orbitals are not the only hydrogen states that are allowed. Any (normalizable) linear combination of such states is itself another possible quantum state of the hydrogen atom. And since there is degeneracy in the hydrogen spectrum (i.e., many independent states with the same energy), it is even possible to find linear combinations of $\psi_{nlm}$ that are good quantum states with the same energy but have very different spatial structures than the $\psi_{nlm}$'s. These other linear combinations are ones that you find when you solve the hydrogen Schrodigner equation by separating in other coordinate systems.

---

When we do the standard thing and separate the hydrogen Schrodinger equation in spherical coordinates, we are effectively finding the eigenstates of the hydrogen hamiltonian that are also eigenstates of the angular momentum operators $L^2$ and $L_z$. Any linear combination of eigenstates with the same energy will also be an eigenstate with that same energy.

For instance, consider the eigenstates of energy $E_2 = -\textrm{Ry}/4$, which in the standard representation are labeled $\psi_{200}$, $\psi_{21,-1}$, $\psi_{210}$, and $\psi_{201}$, where the subscripts correspond to $n$, $l$, and $m$ quantum numbers: $l$ and $m$ are related to definite values of angular momentum these states have. For the $l=1$ states, chemists sometimes like to talk about $p_x$, $p_y$, and $p_z$ orbitals rather than the $m=-1$, $m=0$, and $m=1$ states, and these correspond to \begin{align} p_x&\to \psi_{n11}(\vec{r}) -\psi_{n1,-1}(\vec{r})\,,\\ p_y&\to \psi_{n11}(\vec{r}) +\psi_{n1,-1}(\vec{r})\,,\\ p_z&\to \psi_{n10}(\vec{r}) -\psi_{n1,-1}(\vec{r})\,, \end{align} up to normalization. These are not the states you get by separating the in spherical coordinates. However, they are perfectly good orbitals, because they are eigenstates of the Hamiltonian and therefore states of definite energy. (See pictures below: we show the $p_x$, $p_y$, $p_z$ orbitals and the $l=1$ ($m=-1$, $m=0$, and $m=-1$) orbitals in the $n=2$ energy subspace. These have different spatial structures.)

When we separate the differential equation in different coordinate systems, we are no longer finding the eigenstates of $H$ that are also eigenstates of $L_z$ and $L^2$; rather, the solutions we get will be linear combinations of those states, and so they will show different spatial structures. This is fine. They are perfectly good quantum states, and in fact perfectly good states of definite energy.

Answer 2

I think the gist of your question is being buried by the complexity of the system in question. Let's back to the fundamentals.

The probability density to find the electron in the instant $t$ is given by the modulus squared of the wave function

$$ \rho(\mathbf r,t)= |\Psi(\mathbf r,t)|^2. $$

The wave function $\Psi(\mathbf r,t)$ is usually unknown, unless we have some information about the system or we make some considerations about it. One usual assumption is to consider that the system was initially in the ground state. With this assumption,

$$ \Psi(\mathbf r,0)=\psi_{000}( r), $$

and the wave function could be determined in later times solving the Schrodinger equation.

Now, to solve the Schrodinger equation, it is clever to write the wave function as a linear combination of eigenstates of the Hamiltonian. In this case if we write

$$ \Psi(\mathbf r,t) = \sum_{n,l,m} c_{nlm}(t)\psi_{nlm}(r,\theta,\phi) $$

It is easy to show that $c_{nlm}(t)=c_{nlm}(0)e^{-iE_nt/\hbar}$, and by the initial condition, the only nonzero coefficient in the expansion would be $c_{000}$.

Now, we could choose any other basis to expand the wave function. Let's suppose we have a set of eigenfunctions $\phi_{esg}(\xi_1,\xi_2,\xi_3)$ with quantum numbers $e,s,g$ in an arbitrary coordinate system $(\xi_1,\xi_2,\xi_3)$. If course the associated eigenvalues $\epsilon_{esg}$ would give the same values given by $E_n$ (with different labels, given by the new quantum numbers), since the eigenvalues of an operator is basis independent. Expanding the wave function, we will have

$$ \Psi(\mathbf r,t) = \sum_{esg} b_{esg}(t) \phi_{esg}(\xi_1,\xi_2,\xi_3), $$

where $b_{esg}(t)=b_{esg}(0)e^{-i\epsilon_{esg}t/\hbar,}$. Let's suppose the in this labeling, the ground state energy $E_0= -Ry$ is given by $\epsilon_{001}$ and $\epsilon_{100}$, i.e., $\epsilon_{001}=\epsilon_{100} = -R_y$. Then we will need to solve

$$ b_{001}\phi_{001}(\mathbf \xi) + b_{100}\phi_{100}(\mathbf \xi) = \psi_{000}(r) $$

for the coefficients $b_{001}$ and $b_{100}$. Now, it could take a lot of time to discover how to relate the coordinates $\xi_j$ with the spherical coordinates, to write the function $\psi_{000}$ in the $\xi$ basis and to solve the integrals like

$$ \int \phi_{001}(\mathbf \xi)\psi_{000}(\mathbf \xi) \, d^3\mathbf \xi. $$

After all this labor, we would have a quantum state

$$ \Psi(\xi,t) = (b_{001}\phi_{001}(\xi)+b_{100}\phi_{100}(\xi))e^{-i\,\text{Ry}\,t/\hbar} $$

that in the end, describes the same orbital and the same probability density that we would have in the spherical coordinate system.

---

It doesn't matter the eigenbasis we choose to represent the wave function. It is important, however, to know and understand what initial conditions we are considering, as emphasized by Radost Waszkiewicz in the comments.

Answer 3

If these various coordinate‐system “orbitals” are just different basis functions for the same physical eigenstates, how do we reconcile their radically different individual shapes with the fact that the underlying probability density of the electron in the H-atom $|Ψ|^2$ must be the same? In particular, how would we demonstrate (analytically or numerically) that $|Ψ_{0,1,0}|^2$ computed in any of these coordinate systems yields the identical 3D electron‐density distribution? ... Why [do] different and non-conventional coordinate systems for solving the Schrodinger equation apparently lead to different orbital shapes and probability density ($|\Psi|^2$) of finding a electron at a given position?

Respectfully, these questions are demonstrating a fundamental confusion about the nature of physical states $|\Psi\rangle$.

You can't "solve the [time-independent] Schrodinger equation", all by itself, to derive "the probability density $|\Psi|^2$ of finding a[n] electron at a given position". The TI Schrodinger equation doesn't give you that information. What the TI Schrodinger equation $\hat{H} \Psi = E \Psi$ gives you is a set of energy eigenvalues $\{E_i\}$, and for each energy eigenvalue $E_i$ an eigenspace - a subspace of the Hilbert space - of physical states with that energy $E_i$. That's it. It does not in general specify the state of any particular physical electron; that requires additional information about the initial conditions. (If we make the additional assumption that the electron is in thermal equilibrium at some temperature $T$, then that does specify the state of the electron. But this assumption doesn't always hold.)

If an eigenspace corresponding to an energy eigenvalue $E_i$ is degenerate (i.e. has dimension greater than 1), then there are multiple possible bases for that eigenspace. What you call "solving the Schrodinger equation in different coordinate systems" is really "separating the Schrodinger equation in different coordinate systems". This process can indeed result in different bases for the same vector space. But that's fine; as is always the case in linear algebra, you can decompose the same vector space into many different bases.

A given physical state $|\Psi\rangle$ - which, again, cannot be derived solely by "solving the Schrodinger equation" - has a unique real-space probability distribution $|\Psi({\bf x})|^2 = |\langle {\bf x} | \Psi\rangle|^2$. This probability distribution will be the same regardless of which basis/coordinate system we choose to decompose the state $|\Psi\rangle$ into (although it will be expressed as a different linear combination of basis vectors in different bases). Again, there's nothing deeper going on here than the fact that you can always choose to assign a (higher-than-1-dimensional) vector space with different bases.

Edit: You are certainly correct that the physical shape of the real-space probability density $|\Psi({\bf x})|^2$ cannot depend on our choice of coordinate functions. So if Lamoureux and Ogilvie derive a state that they choose to call "$\Psi_{0,1,0}$" in a paraboloid coordinate system whose real-space probability density differs from that of the usual spherical-coordinate orbitals, then that simply means that they are referring to a different physical state using confusingly similar notation. (Note that it isn't even clear what "$\Psi_{0,1,0}$" would mean in the standard spherical coordinates; that can't represent a state with quantum numbers $n = 0, l = 1, m = 0$, because those putative quantum numbers don't satisfy the constraint that $l < n$.) So their "paraboloid orbitals" are simply not the same basis states as the usual spherical orbitals, even if they use a similar numbering scheme.