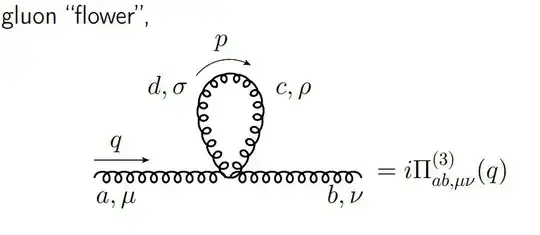
I am consulting https://users.jyu.fi/~htpaukku/QFTII/Week12.pdf for the gluon self-energy. Eq. (3.200) contains the contribution of the gluon flower graph:
The contribution comes out to $$ -g^2\delta_{ab}\eta_{\mu\nu}C_G\int \frac{d^4p}{(2\pi)^4}\frac{1}{p^2} $$ In dim-reg, the momentum integral is zero (see here). But if we use cutoff regularization, the integral goes as $\Lambda^2$ and, therefore, it appears as if the (zero) gluon mass gets renormalized. This may appear bonkers because the gluon must be massless. However, we know that Yang-Mills dynamically generates a mass-gap. So maybe this isn't as bonkers as it appears. My question is why isn't this considered as a way to generate the mass-gap?