Computing QED corrections to the hydrogen atom in a fully relativistic two-particle formalism is messy; in principle, it could be done starting from the Bethe-Salpeter equation, in practice, it is very hard.
If you take the nuclear mass to be infinite in a first approximation, then the effect of the nucleus (as an external Coulomb potential) can be built into your fermion creation/annihilation operators:
$$
\Psi(x)=\sum_{\substack{n \\ E_n>0}}a_n\psi_n(x)+\sum_{\substack{n \\ E_n<0}}b^\dagger_n\psi_n(x) \ ,
$$
where $\psi_n(x)=\phi_n(\vec{r})\exp(-iE_nt)$ are solutions of the (first-quantized) Dirac equation:
$$
\left[\vec{\alpha}\cdot\vec{p}+\beta m-|e|\int\mathrm{d}^3r'\frac{\rho_\text{N}(\vec{r}{}')}{4\pi|\vec{r}-\vec{r}{}'|}I\right]\phi_n(\vec{r})=E_n\phi_n(\vec{r}) \ .
$$
This defines the so-called Furry representation. For a point-like nucleus
$$
-|e|\int\mathrm{d}^3r'\frac{\rho_\text{N}(\vec{r}{}')}{4\pi|\vec{r}-\vec{r}{}'|}=-\frac{Z\alpha}{r} \ ,
$$
and the Dirac equation can be solved analytically. Then you can set up the fermion propagator, the diagram rules, and go on almost like in the non-interacting case.
Using these solutions, the QED corrections to the atomic energy levels can be obtained from e.g. the Gell-Mann - Low (GML) formula, which relates the energy shift to $S$-matrix elements. In leading (one-loop) order, two $S$-matrix diagrams contribute, belonging to bound-electron self-energy (with a mass counterterm understood) and vacuum polarization:
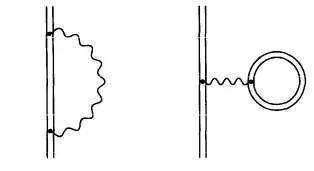
The double lines correspond to the fermion propagator in the external Coulomb field of the nucleus. You can process these diagrams to a certain degree, but their exact evaluation can only be done numerically. If your system is predominantly non-relativistic (like the hydrogen atom), then you can start doing expansions in the binding parameter $Z\alpha$, and this will lead you to the ${\cal{O}}(m\alpha(Z\alpha)^4, \, m\alpha(Z\alpha)^4\ln(Z\alpha))$ textbook result for the Lamb shift (see e.g. Ch. 15 of The Theory of Photons and Electrons by Jauch & Rohrlich); the expectation value of the Uehling potential is a tiny part of this shift, originating from the second diagram. For strongly relativistic systems (hydrogen-like ions with large $Z$), you have no choice but to calculate the fully relativistic expressions numerically, but that is very difficult; see e.g. this review by Mohr, Plunien and Soff to get a taste, and for a discussion on the GML formula. If you already calculate everything fully numerically, than the assumption of a point-like nucleus is not that important, and you can incorporate some finite density model.
Treating the nucleus explicitly as a particle is possible for a spin $1/2$ nucleus, but for other nuclear spins, I am not sure if there is even a rigorous first-principles theory (there is possibly one for spin $0$, but for higher spins, there are most likely only effective theories working with non-relativistic wave functions). Recoil corrections can be extracted from Coulomb and transverse photon exchange diagrams in the Bethe-Salpeter formalism; in the low-energy approximation, these contribute to the QED energy shift at ${\cal{O}}(m(Z\alpha)^5(m/M))$ (there is no $\alpha$ here, only $Z\alpha$, signalling that these are non-radiative QED effects, not loop corrections).
