According to the energy-time uncertainty principle:
$$
\Delta E \, \Delta t \approx \hbar
$$
Since $\Delta E = \hbar \, \Delta \omega$, it follows that:
$$
\Delta t \approx \frac{1}{\Delta \omega}
$$
This means that if the incident photons have frequency $\omega \ne \omega_0$ (the transition frequency), the atom can still undergo a transition with small probability, provided the interaction time $\Delta t$ is short enough. In this context, $\Delta \omega = \omega - \omega_0$ effectively represents the frequency width of the transition.
As a back-of-the-envelope estimate, consider a gamma-ray photon with wavelength mismatch $\Delta \lambda \sim 10^{-13} \, \text{m}$. Then the frequency mismatch is:
$$
\Delta f = \frac{c}{\Delta\lambda} = \frac{3 \times 10^8}{10^{-13}} = 10^{21} \, \text{Hz}
$$
So the angular frequency mismatch is:
$$
\Delta \omega \sim 10^{21} \, \text{rad/s}
$$
and then:
$$
\Delta t \sim 10^{-21} \text{ to } 10^{-23} \, \text{s}
$$
These are typical timescales for strong interactions. So yes, off-resonant transitions are possible, but highly suppressed and require extremely short interaction times. In practice, photon absorption is efficient only when $\omega \approx \omega_0$, i.e., on resonance.
Edit: My previous answer used the uncertainty principle and assumed that the levels have width, but the OP specifically mentioned sharp levels (i.e., no width), so here is the mathematical situation:
I'll follow Griffiths' Intro to Quantum Mechanics, 1st ed., Chapter 9, p. 298 onward.
For a two-level system with states $|g\rangle$ (ground) and $|e\rangle$ (excited), the wavefunction under a time-dependent perturbation $H'(t)$ evolves as:
$$
\Psi(t) = c_g(t) \psi_g e^{-i E_g t/\hbar} + c_e(t) \psi_e e^{-i E_e t/\hbar}
$$
Plugging this into the Schrödinger equation with $H = H_0 + H'(t)$ gives:
$$
\dot c_g(t) = \frac{-i}{\hbar} \left[ H'_{gg} c_g(t) + H'_{ge} c_e(t) e^{-i \omega_0 t} \right]
$$
$$
\dot c_e(t) = \frac{-i}{\hbar} \left[ H'_{eg} c_g(t) e^{i \omega_0 t} + H'_{ee} c_e(t) \right]
$$
where $\omega_0 = (E_e - E_g)/\hbar$, and $H'_{eg}, H'_{ee}$, etc., are the matrix elements, e.g., $H'_{eg} = \langle e|H'|g \rangle$.
Now assume the interaction is turned on at $t = 0$ and lasts for time $t$, and that the system starts in state $|g\rangle$, so $c_g(0) = 1$, $c_e(0) = 0$.
Griffiths is vague on the next step, but for an interaction Hamiltonian of the form
$$
H'(t) \sim e \vec{r} \cos(\omega t)
$$
and if the states $\psi_g$ and $\psi_e$ are parity eigenstates (e.g., hydrogen 1s and 2p), then $\langle g | \vec{r} | g \rangle = \langle e | \vec{r} | e \rangle = 0$ by parity. So $H'_{gg}(t) = H'_{ee}(t) = 0$, and only the off-diagonal terms contribute.
To first order in time-dependent perturbation theory (see p. 302):
$$
c_e(t) \approx \frac{-i}{\hbar} \int_0^t H'_{eg}(t') e^{i \omega_0 t'} dt'
$$
Assume $H'_{eg}(t) = V_{eg} \cos(\omega t)$, where $V_{eg} = \langle e | V(\vec{r}) | g \rangle$. Then:
$$
c_e(t) = \frac{-i V_{eg}}{\hbar} \int_0^t \cos(\omega t') e^{i \omega_0 t'} dt'
$$
Using $\cos(\omega t') = \frac{1}{2} \left( e^{i \omega t'} + e^{-i \omega t'} \right)$:
$$
c_e(t) = \frac{-i V_{eg}}{2\hbar} \int_0^t \left( e^{i(\omega + \omega_0)t'} + e^{i(\omega_0 - \omega)t'} \right) dt'
$$
Integration yields:
$$
c_e(t) = \frac{-i V_{eg}}{2\hbar} \left[ \frac{e^{i(\omega + \omega_0)t} - 1}{i(\omega + \omega_0)} + \frac{e^{i(\omega_0 - \omega)t} - 1}{i(\omega_0 - \omega)} \right]
$$
Simplifying:
$$
c_e(t) = \frac{V_{eg}}{2\hbar} \left[ \frac{1 - e^{i(\omega_0 - \omega)t}}{\omega_0 - \omega} + \frac{1 - e^{i(\omega + \omega_0)t}}{\omega + \omega_0} \right]
$$
If $\omega_0 + \omega \gg |\omega_0 - \omega|$, i.e., the driving frequency is near resonance, we can neglect the second term:
$$
c_e(t) \approx -i \frac{V_{eg}}{\hbar} \cdot \frac{\sin\left(\frac{(\omega_0 - \omega)t}{2}\right)}{\omega_0 - \omega} e^{i(\omega_0 - \omega)t/2}
$$
Then the transition probability becomes:
$$
P_{g \to e}(t) = |c_e(t)|^2 \approx \left( \frac{V_{eg}}{\hbar} \right)^2 \cdot \frac{\sin^2\left( \frac{(\omega_0 - \omega)t}{2} \right)}{(\omega_0 - \omega)^2}
$$
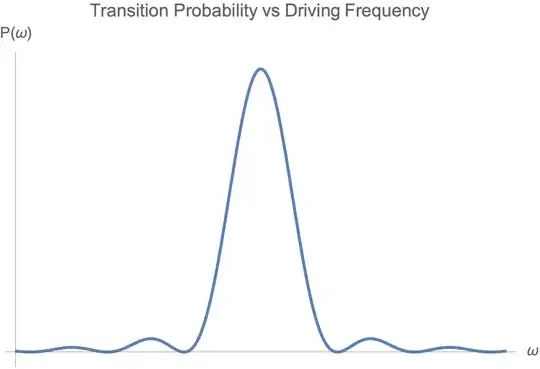
This is the familiar sinc-squared shape, sharply peaked at $\omega = \omega_0$.
So even with sharp levels, off-resonant transitions are allowed mathematically. I made a quick plot of $P(\omega)$ vs $\omega$, and you can see the sharp peak in the figure below: