Can the proper time go backwards?

Question

I have computed radial time-like geodesics for the Schwarzschild interior solution beyond the Buchdahl limit. While checking the result I noticed some strange behavior of the proper time. It seems to go backwards when the ratio $r_S/R$ exceeds $8/9$ (the Buchdahl limit). Here is my calculation:

For a static spherically symmetric spacetime described by the length element $$ ds^2=e^{2\nu}c^2dt^2-e^{2\lambda} dr^2-r^2 d\Omega^2 ,\tag{1}$$ the geodesics equation for radially ($d\Omega=0$) in-falling time-like geodesic is $${e}^{2\nu+2\lambda}~\frac{\dot{r}^2}{c^2}=k^2-{e}^{2\nu} \tag{2}.$$ In this equation, k is the constant of motion, $k={e}^{2\nu}\cdot\dot{t}$, and the dot is the derivative with respect to the proper time $\tau$. Using the dimensionless variable $\xi \equiv r/R$ and the parameter $\alpha\equiv r_{S}/R$, the Schwarzschild interior metric reads $$e^{-\lambda} =\sqrt{1-\alpha~\xi^2},~~~~~e^{\nu} = 3/2~\sqrt{1-\alpha}-1/2~\sqrt{1-\alpha~\xi^2}, \tag{3}$$ The geodesics equation ($2$) can be solved analytically by integration: $$\int_\xi^1 \frac{{\rm e}^{\nu+\lambda}~d\xi}{\sqrt{k^2-{\rm e}^{2\nu}}}=-\frac{1}{R}\int_{s}^{s_1} ds=\frac{c}{R}~(\tau-\tau_1).\tag{4}$$ If we set the integration constant $\tau_1$ to zero, the relation between proper time $\tau$ and dimensionless radius $\xi$ is given by $$\tau(\xi)=\frac{R}{c}\frac{2}{\sqrt{\alpha}}\frac{1}{9(1-\alpha)-(1-2k)^2}\bigg\{(3\sqrt{1-a}+1)\big[\rm{F}\big(\varphi(1)|m\big)-\rm{F}\big(\varphi(\xi)|m\big)\big]-2\big[\Pi\big(n,\varphi(1)|m\big)-\Pi\big(n,\varphi(\xi)|m\big)\big]\bigg\} \tag{5}$$ where $\rm{F(x|m)}$ and $\Pi(n;x|m)$ are elliptic integrals of the first and third kind, respectively, and the variable $\varphi$ and the constants $n$ and $m$ are defined as $$\varphi(\xi)\equiv\arcsin{\sqrt{\frac{(3\sqrt{1-\alpha}+1-2 k)\cdot(\sqrt{1-\alpha \xi^2}-1)}{(3\sqrt{1-\alpha}-1-2 k)\cdot(\sqrt{1-\alpha \xi^2}+1)}}},\tag{6}\\n\equiv\frac{3\sqrt{1-\alpha}-1-2 k}{3\sqrt{1-\alpha}+1-2 k},~~~m\equiv\frac{9(1-\alpha)-(1+2 k)^2}{9(1-\alpha)-(1-2 k)^2}.$$ It is the same result as in the paper A relativistic gravity train.

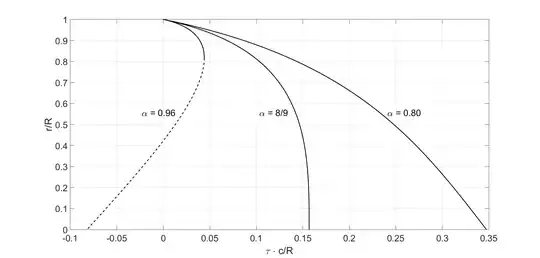
The graph below shows the relation between $r$ and $\tau$ in dimensionless units ($\tau R/c, r/R$) for three $\alpha$ values and $k=1$ (zero velocity at infinity).

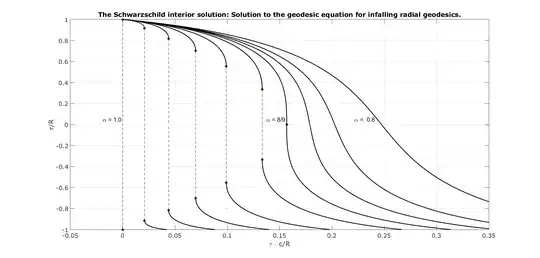
We can see that the proper time to reach the center ($\xi=0$) from the boundary ($\xi=1$) is finite, as expected, but its behavior depends on $\alpha$: for $\alpha<8/9$ it goes forward, for $\alpha=8/9$ (Buchdahl bound) it stops, and for $\alpha>8/9$ it seems to go backward (dashed part of the line).

If proper time cannot go back, then one must conclude that the radial in-falling time-like geodesics in Schwarzschild interior spacetime end on the two-sphere with curvature radius defined by $e^{\nu}(\xi_0(\alpha))=0$, i.e. $r_0=R\sqrt{9-8/\alpha}$.

Would this conclusion be correct?

Answer 1

The author's conclusion is not correct. Proper time does not stop at the event horizon. Something else happens. I hypothesize that when the radial component of the four velocity, $dr/ds$, becomes infinite, the infalling geodesic instantly switches to its antipodal counterpart, the outgoing geodesics, like a worldline of transcendent tachyon would do.

As the parameter $\alpha~(\equiv r_{S}/R)$ approaches $1$ (the Schwarzschild event horizon), the result is the same as that described by Gerard t’Hooft in his paper What Happens in a Black Hole When a Particle Meets Its Antipode: "(…) a curve that crosses the horizon from region I into region II does not enter the 'interior' of the black hole but instead goes directly to the points outside the antipode (...).", page $5$.

The picture below shows the instantaneous switch to antipodal points (vertical dotted lines) and geodesics that started at rest in infinity (solid lines). These geodesics result in a velocity equal to the $\sqrt{\alpha}$ upon crossing the star's surface ($r=R$).