0

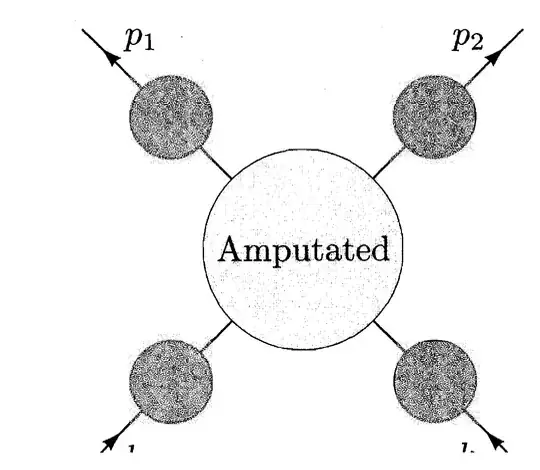
In Peskin & Schroeder's book (chapter 7.2,p227), they claim that the exact 4-point function, expressed by $$ \left( \prod_{i=1}^{2} \int d^4 x_i \, e^{i p_i \cdot x_i} \right) \left( \prod_{i=1}^{2} \int d^4 y_i \, e^{-i k_i \cdot y_i} \right) \langle \Omega | T \{ \phi(x_1) \phi(x_2) \phi(y_1) \phi(y_2) \} | \Omega \rangle \tag{p.227} $$ can be translated into the diagram (Fig. 7.4)

the momentum diagram

My question is: How do we derive the diagram in the picture solely from the exact 4-point function above?

I try to understand this using the diagrammatic interpretation of 4-point function in position space, but I fail because all diagram in position space end at some point and I cannot related them to the diagram in momentum space.

This question can be seen as a follow up question of this one, they are related, but this question focus more on the diagrammatic interpretation of the problem.

Qmechanic
  • 220,844
Interstellar
  • 1,593

2 Answers2

2

  1. In Fig. 7.4 P&S is merely defining an amputated connected $n$-point function as a connected $n$-point function stripped of $n$ external connected propagators.

    This is possible since it is known$^{\dagger}$ that a connected $n$-point function is (a sum of possible) trees of connected propagators and amputated 1PI vertex functions, cf. e.g. my Phys.SE answer here.

    By the way, P&S also discuss amputations on p.113-114.

  2. As for the formula on p.227 mentioned by OP, it is a Fourier transform of the connected 4-point function.

$^{\dagger}$Fine print: Here it is implicitly assumed that there are no tadpoles/1-point functions. This holds for $\phi^4$ theory because of $\mathbb{Z}_2$-symmetry.

Qmechanic
  • 220,844
1

To go from position to momentum space, you have to Fourier transform. That involves an integral over the entire real space. In that sense, a momentum space correlation function is a superposition of real space correlation functions at every starting and end points.

That said, the incident/outgoing legs are still created/annihilated by some operators with definite momenta, much like their real space cousins that have definite positions. You can view that as "line ending".

On a separate matter, I would not use the term "tadpole" for the line ending at these "external" operators. (External as in being explicitly featured in the correlation function $\langle \phi \dots \rangle$.) A tadpole usually refers to the situation where a line just somehow ends without an external operator to create/annihilate it. I think @Qmechanic is applying the term in exactly this sense, but perhaps misunderstood what the OP means by "line ending".

T.P. Ho
  • 777