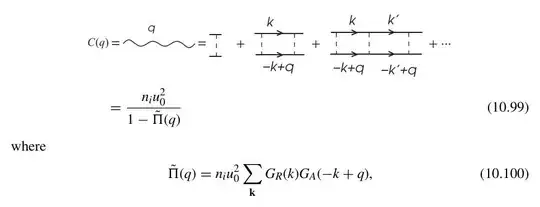I'm current following Piers Coleman's Many-Body Physics to understand the diagrammatic method for Anderson localization (weak localization)
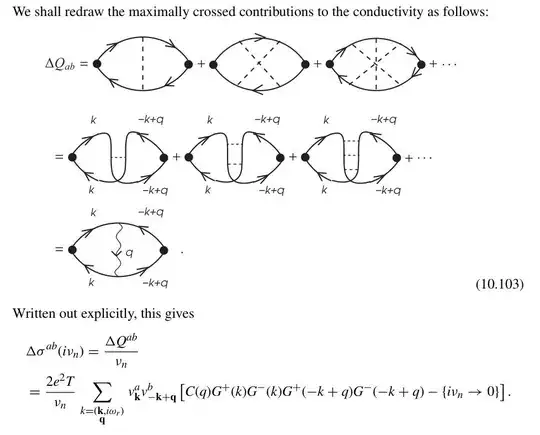
The diagrams are as follows.
where the dashed line is the impurity scattering $n_i |u(\mathbf{p} - \mathbf{p}')|^2$ and the wavy line is the Cooperon.
I have no idea how I can get the second line of eqn (10.103), since the impurity scattering does not change Matsubara frequency, but from the first diagram in the second line we can see that the impurity scattering line carries a momentum $w = 2k - q$, but it cannot have any frequency part. So it seems that the frequency part of $q$ is not free, it must be $q^0 = 2 k^0 = 2i \omega_r$. That how I interpret these diagrams.
The calculate proceeded as ($q$ was set to 0 in the conduction line to get the most singular contribution. Though I don't know why, but let's just follow the calculation):
$$ \Delta \sigma^{ab}(i \nu_n) = \frac{2e^2T}{\nu_n} \sum_{\mathbf{q}} C(q) \sum_{k} v^a_{\mathbf{k}} v^b_{-\mathbf{k}} [(G^+(k))^2(G^-(k))^2 - \{i\nu_n \to 0\}]. \tag{10.104} $$
The author then declared that $\sum_{k} v^a_{\mathbf{k}} v^b_{-\mathbf{k}} = \frac{-\nu_n}{2\pi T} \frac{ne^2}{m} \delta^{ab}\int \mathrm{d} \epsilon$. In my opinion, that's totally nonsense. Since $q^0$ is related to $k^0$, how can we perform the summation over $k$ first? And how could Matsubara frequency come into this summation?
And in the following calculation, it seems that the author considered $q = (\mathbf{q}, i\nu_n)$, where $i \nu_n$ is the frequency of external source(for probing the electrical current). Well then, looking back at the second line of eqn (10.103), the impurity scattering line then carried a nonzero Matsubara frequency.
Sorry for presenting two questions about this book in one week, but I found this book extremely confusing (especially this Chapter on transportation theory).