I was reading this question and I was confused about the emf across the rod MN.
Part in consideration for this question:
Now consider a conducting bar of length l sliding along two parallel conducting rails .....
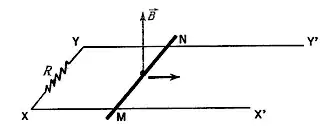
If we know apply some force on the bar ........ Faraday's law says the change in magnetic flux, equal to Blv ...... Now let's use a different reasoning. The Lorentz force law implies that the positive charges in .......induced in the bar equal to $V_M−V_N$ = Blv .
It seems as if it is accepted by everyone on that the emf across the rod will be Blv (which the OP also assumed and used to put forth his arguments). This isn't obvious to me.
Wouldn't it be the sum of both motional and induced emf?
- There exists time varying magnetic flux through the circuit. Hence, a induced emf.
- There also exists the Lorentz force on the rod. Hence, a motional emf.
Why won't the emf across the rod be the sum of both the emfs?
When would this be the case?