Confusion about induced emf vs motional emf

Question

Faraday's law says that the change in magnetic flux through the area enclosed by a wire loop induced an emf in the circuit. What exactly is this induced emf?

If I understand correctly, it is the amount of work done on a unit charge which makes 1 full turn around the loop by the induced electric field inside the wire (*).

In electrostatics, the electric field in a wire loop is conservative (why?), so an electron which makes a full turn around wire loses as much energy as it gains. In otherwords the emf of the circuit is zero, if I understand correctly.

However, apparently in a circuit with an induced emf, an electron which makes one full loop can gain energy. So as electrons continue to travel around the circuit, they gain more and more energy. In otherwords, the induced emf is due to an induced electric field in the wire which is nonconservative. Does this make any sense?

---

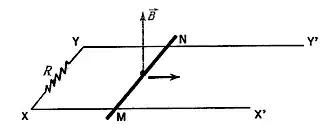
Now consider a conducting bar of length $l$ sliding along two parallel conducting rails which are connected by a resistance $R$. The circuit is subjected to a uniform magnetic field perpindicular to the plane of the circuit, as below.

If we know apply some force on the bar such that it moves along the rails with constant velocity $v$ to the right. Faraday's law says the change in magnetic flux, equal to $Blv$ (with area vector of the circuit pointing parallel to B), induces an emf in the circuit producing a current in the clockwise direction, and the emf is equal to $-Blv$. The current in the circuit is then $I=-Blv/R$ measured in the counterclockwise sense.

Now let's use a different reasoning.

The lorentz force law implies that the positive charges in the moving bar are pushed towards point $M$ and the negative charges towards (the electrons) towards point $N$. We thus get an electric field $E$ inside the bar pointing from $M$ to $N$. When the charges reach equilibrium inside the bar, we have that $qE=qvB$ thus $E=Bv$. We thus get a "motional emf" induced in the bar equal to $V_M-V_N=Blv$. In order to arrive at the same answer for the current, we would thus need that the voltage drop across the resistor is equal to the voltage increase across the conducting bar, equivalently that the work done on a charge making a full loop is zero.

However, doesn't this contradict our definition (*) of induced emf?

Answer 1

In electrostatics, the electric field in a wire loop is conservative (why?) so an electron which makes a full turn around wire loses as much energy as it gains. In other words the emf of the circuit is zero, if I understand correctly

Electrostatic field is conservative because if we move a charge from point A to B, the work done is irrespective of the path taken.

The easiest way to prove this is by taking a point $q$ charge, taking it away to some point and then bringing it back to initial point (without increasing its kinetic energy).

For electrostatic field:

$W_{ext}=-q\Delta V=-q(\oint_{closed-loop}\vec E \cdot {d\vec{l})}=-q(-\frac{\mathrm{d}\phi }{\mathrm{d} t})=0 \\ \Rightarrow W=0$

This implies that irrespective of the path taken, work done is always $0$ in an electrostatic field when charge is brought back to initial position since $\frac{d \phi}{dt} $ is always $0$.

For induced electric field:

$W_{ext}=-q\Delta V=-q(\oint_{closed-loop}\vec E \cdot {d\vec{l}})=-q(-\frac{\mathrm{d}\phi }{\mathrm{d} t}) \neq 0 \\ \Rightarrow W \neq 0$

Here $\frac{d\phi}{dt}$ depend on the path taken.

Hence electrostatic field is conservative, but induced electric field is not.

In otherwords the emf of the circuit is zero, if I understand correctly.

Since there is no battery, there is no EMF. In the above case, we are making the charge move around. So there is no need of EMF.

If you were asking about a circuit with a battery, then the EMF is provided by the battery.

However, apparently in a circuit with an induced emf, an electron which makes one full loop can gain energy. So as electrons continue to travel around the circuit, they gain more and more energy. In otherwords, the induced emf is due to an induced electric field in the wire which is nonconservative. Does this make any sense?

The work done in changing the magnetic field is transferred to the electrons in the conductor, which gives them energy to move around. This is a consequence of Law of Conservation of Energy.

Now, main question:

... However, doesn't this contradict our definition (*) of induced emf?**

No. Because it is not rigorous to use Faraday's Law here in the first place.

$\oint_{c}\vec E \cdot {d\vec{l}}=-\frac{d}{dt}\int_{s} \vec B \cdot {d\vec{l}} $

is the common version of Faradays's Law. It is rigorously correct only if $\vec E$ represents the electric field in the rest frame of each segment $d\vec l$ of the path of integration. This is definitely not true is the case of motional EMF.

It is necessary to note that only a time-varying magnetic field induces a circulating non-conservative electric field in the rest frame of the laboratory. A changing flux does not induce an electric field. Hence in case of motional EMF, no electric field is induced in the laboratory frame(where rod is in motion). Hence technically $\oint_{c}\vec E \cdot {d\vec{l}} = 0$ here.

A potential difference is maintained across the rod by the EMF and Lorentz force maintains that EMF. Using $-\frac{d}{dt}\int_{s} \vec B \cdot {d\vec{l}} $ here is just a convenient way of calculating the EMF.

Source: A Student's Guide to Maxwell's Equations -- Daniel Fleisch

Answer 2

I think that your difficulty arises at the end of your penultimate paragraph...

"In order to arrive at the same answer for the current, we would thus need that the voltage drop across the resistor is equal to the voltage increase across the conducting bar, equivalently that the work done on a charge making a full loop is zero."

There is a potential difference between M and N (i.e. between X and Y) due to separation of charges as as you explain. Around the loop MXYNM the potential rises along NM and falls by the same amount along XY, so the net work done by separated charges on a test charge taken round the loop is zero. But work is done by the magnetic Lorentz force as the test charge goes through NM. So the work done on a test charge taken round the loop is not zero. It is only the 'electrostatic' work that is zero.

Answer 3

(In the following, I address the first section of the OP's post.)

In electrostatics, the electric field in a wire loop is conservative (why?)

In electrostatics, the electric field in a wire (conductor) is zero. Remember, no charge is moving in the electrostatic case. Since charge is mobile in a conductor, if all charge were static at one moment and there were an electric field within the conductor, charge would accelerate and thus, in the next moment, charge would be moving in contradiction to the assumption that no charge is moving.

And yes, in the electrostatic case, the electric field is conservative.

so an electron which makes a full turn around wire loses as much energy as it gains

Since there's no electric field within the conductor (remember, electrostatic case), the wire is an equipotential. How then would a charge gain potential energy if there's no change in potential along the wire?

However, apparently in a circuit with an induced emf, an electron which makes one full loop can gain energy.

Yes and no. First, it is true that a changing magnetic field is associated with electric field lines that form closed loops. If one moves a unit test charge once around an appropriate closed path in such a changing magnetic field, there will be an associated net work and the magnitude of this work is the emf associated with the closed loop.

However, when you introduce a conducting wire loop (we'll assume with finite conductivity), mobile charge is accelerated by the induced electric field and so, one can have a current through the wire and thus, via Ohm's law, an electric field through the wire. Further, and importantly, there will be energy lost due to Joule heating.

Now consider the case that the rate of change of the magnetic field threading the wire loop is constant. If charge gains energy once around the loop, see that this implies an increasing current. If charge loses energy once around the loop, see that this implies decreasing current. Clearly, there must a value of current for which charge neither gains nor loses energy once around the loop and this is the steady state current value.

In steady state, the energy lost due to heating the wire equals the energy gained once around due to the induced electric field.

Note that if the wire is ideal (infinite conductivity AKA zero resistance), there is no steady state current value; the current must change at precisely the rate such that the changing (current) induced magnetic field threading the loop cancels the external changing magnetic field threading the loop.