In section 10.4 of Piers Coleman's book Introduction to Many-Body Physics, the electron density response function in present of impurity scattering was calculated.
He calculated the following Feynman diagrams(in imaginary time formalism)
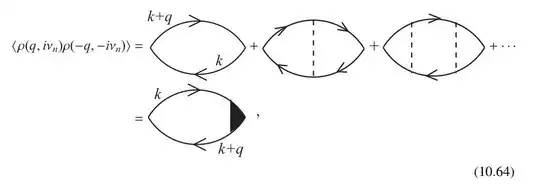where the dashed lines were impurity induced attraction and electron propagators in these diagrams were already corrected by first order impurity scattering effect. i.e.
$$ G(\mathbf{k}, i\omega_r) = \frac{1}{i \omega_r - \epsilon_{\mathbf{k}} + (i/2\tau) \operatorname{sgn}\omega_r} $$
There are two things in the calculation which I am particularly confused about.
The first question is physical. The Dyson equation for vertex correction is:
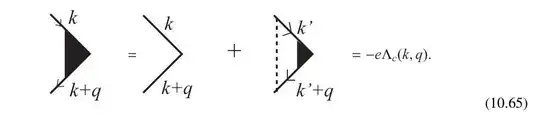That is:
$$
\Lambda_c(k, q) = 1 + n_i \sum_{\mathbf{k}'} |u(\mathbf{k} - \mathbf{k}')|^2 G(k' + q) G(k') \Lambda_c(k', q) \tag{10.67}
$$
After approximating $u(\mathbf{k} - \mathbf{k}') = u_0$(then $\Lambda(k, q) = \Lambda(i\omega_w, q)$), we get $\Lambda(i\omega_r, q) = [1 - \Pi(i\omega_r, q)]^{-1}$
,where:
$$
\Pi(i\omega_r, q) = \int \frac{\mathrm{d}\Omega_{\mathbf{v}_F}}{4\pi} \frac{1}{1 + \nu_n \tau - i \mathbf{q} \cdot \mathbf{v}_F \tau} \tag{10.71}
$$
Then, in order to probe long wave-length and long time behavior, assume $q \ll 1/(v_F \tau), \nu_n \tau \ll 1$, expand:
$$
\Pi(q) = \int \frac{\mathrm{d}\Omega_{\mathbf{v}_F}}{4\pi} \left[1 - \nu_n \tau + i \mathbf{q} \cdot \mathbf{v}_F \tau - (\mathbf{q} \cdot \mathbf{v}_F)^2 \tau^2 + \underline{(\nu_n \tau)^2}\right] \tag{10.72}
$$
The term I underlined was ignored in Coleman's book, and with this form of $\Pi(q)$, we got the response function with a diffusion pole. But, since we didn't have some prior assumptions on the relative smallness of these two second order term, why throwing away this term? And surely if we didn't throw away this $(\nu_n \tau)^2$ term, we won't get a diffusion pole. So, how is this approximation(assuming $\nu_n^2 \ll q^2 v_F^2$) related to electron diffusion? What's the physical picture?The second question is (somewhat) technical. In the calculation of imaginary time correlator, Coleman wrote this equation(there is an $e^2$ factor missing, but that's doesn't matter. Typos are everywhere in this books...):
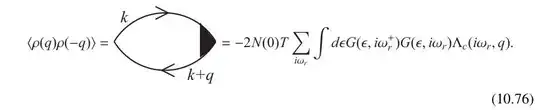where $q = (\mathbf{q}, \nu_n)$ and $\omega_r^+ = \omega_r + \nu_n$. My question is, why did he put two propagator with energy $\epsilon$, instead of one $\epsilon$ and another $\epsilon_{\mathbf{k} + \mathbf{q}} = \epsilon + \mathbf{q} \cdot \mathbf{v}_F$(I'm sure this is not another typo because the following calculation all relies on this fact). In the previous calculation of current response function(section 10.3), it is appropriate to set $\mathbf{q} = 0$ since in any optical conductivity measurement, the light involved is of larger wave-length than the electron's wave-length $\lambda_F$. But here I don't see any rationale for setting $\mathbf{q} = 0$.
