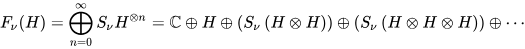You should be familiar with this problem already from elementary quantum mechanics, where the momentum eigen-"state" (better: eigendistribution) $| \vec{p}\rangle$ with $\langle \vec{p} | \vec{p}^{\, \prime }\rangle=\delta^{(3)}(\vec{p}-\vec{p}^{\, \prime})$ is not an element of the Hilbert space $\mathcal{H}$, as $|\psi\rangle \in \mathcal{H}$ requires normalizability $\langle \psi | \psi \rangle < \infty$ with respect to the scalar product defined on $\mathcal{H}$. However, elements of $\mathcal{H}$ can be obtained as linear combinations of the momentum eigendistributions $| \vec{p} \rangle$ of the form
$$
|\psi \rangle = \int\limits_{\mathbb{R}^3} \! d^3p \, f(\vec{p}) \, |\vec{p}\rangle, \tag{1} \label{1}
$$
if the condition
$$
\langle \psi | \psi \rangle = \int\limits_{\mathbb{R}^3} \! d^3p \, |f(\vec{p}) |^2 < \infty \tag{2} \label{2}
$$
is fulfilled. Furthermore, if the normalization condition $\langle \psi | \psi \rangle=1$ holds, the vector given in \eqref{1} represents a quantum mechanical state with momentum space wave function $f(\vec{p})$.
The situation is exactly the same in Fock space (also being a Hilbert space). The vacuum state $|0\rangle $ is a properly normalized state with $\langle 0 | 0\rangle=1$. On the other hand, the one-particle momentum eigendistribution
$$
|\vec{p}\rangle := a^\dagger(\vec{p}) |0 \rangle \tag{3} \label{3}
$$
with
$$
\langle \vec{p} | \vec{p}^{\, \prime} \rangle= \langle 0 |a(\vec{p}) a^\dagger(\vec{p}^{\, \prime}) |0\rangle = \langle 0 |\underbrace{[a(\vec{p}), a^\dagger(\vec{p}^\prime) ]}_{\mathcal{N}(\vec{p}) \, \delta^{(3)}(\vec{p}-\vec{p}^{\, \prime})}|0\rangle = \mathcal{N}(\vec{p}) \delta^{(3)}(\vec{p}-\vec{p}^{\, \prime}), \tag{4} \label{4}
$$
where $\mathcal{N}(\vec{p})$ is a factor associated with your favourite normalization convention. As before, $|\vec{p}\rangle$ defined in \eqref{3} is not an element of the underlying Hilbert space ($=$ Fock space), but (choosing the noncovariant normalization $\mathcal{N}(\vec{p})=1$ for simplicity)
$$
|\psi \rangle = \int\limits_{\mathbb{R}^3} \! d^3p \, f(\vec{p}) | \vec{p} \rangle = \int\limits_{\mathbb{R}^3} \! d^3p \, f(\vec{p}) a^\dagger(\vec{p}) |0\rangle \tag{5} \label{5}
$$
with the condition \eqref{2} is a Fock space element. Choosing $\langle \psi | \psi \rangle=1$, the vector in \eqref{5} represents the most general form of a (pure) one particle state of your theory, where $f(\vec{p})$ is the corresponding momentum space wave function.
If you do not like the creation operators $a^\dagger(\vec{p})$, you may define
$$
a_f^\dagger := \int\limits_{\mathbb{R}^3} \! d^3p \, f(\vec{p}) a^\dagger(\vec{p})\tag{6} \label{6}
$$
creating the normalized state $|\psi \rangle = a_f^\dagger |0\rangle$ given in \eqref{5} from the vacuum state, where the commutation relation
$$
[a_f, a_g^\dagger ]= \int\limits_{\mathbb{R}^3} \! d^3 p \, f^\ast(\vec{p}) g(\vec{p}) \tag{7} \label{7}
$$
holds.
The construction of the two-particle subspace of Fock space should now be clear. Start with the non-normalizable two-particle momentum eigendistributions
$$
|\vec{p}_1, \vec{p}_2 \rangle = a^\dagger(\vec{p}_1) a^\dagger(\vec{p}_2) |0 \rangle \tag{8} \label{8}
$$
and construct the Fock space element
$$
|\chi \rangle = \int\limits_{\mathbb{R}^3} \! d^3p_1 \!\int\limits_{\mathbb{R}^3} \! d^3 p_2 \, f(\vec{p}_1, \vec{p}_2) a^\dagger (\vec{p}_1) a^\dagger(\vec{p}_2) |0\rangle, \tag{9} \label{9}
$$
where $f(\vec{p}_1, \vec{p}_2)=f(\vec{p}_2, \vec{p}_1)$ is symmetric under $\vec{p}_1 \leftrightarrow \vec{p}_2$ (remember $[a^\dagger(\vec{p}_1), a^\dagger(\vec{p}_2) ]=0$) with
$$
\int\limits_{\mathbb{R}^3} \! d^3p_1 \! \int\limits_{\mathbb{R}^3} \! d^3p_2\, |f(\vec{p}_1, \vec{p}_2) |^2 < \infty. \tag{10}
$$