Why are there no purple stars?

Question

Edit: the proposed question about metals does not answer my question, especially that that is about green and no mention of purple.

I have read this question:

Do green stars exists?

where kaine says:

If the average wavelength is right on the green wavelength, blue and yellow and red light will be emitted as well making the light from the star look white.

And this one:

The answer is a result of the way our eyes see combinations of frequencies: Our eyes add up all the colors that come in, and the color we see is the result of this addition.

https://www.astronomy.com/science/why-are-there-no-green-stars-2/

So one of them explains green as being the "middle" of the spectrum, meaning they emit blue, yellow and red in comparable amounts and it becomes a white-appearing star, and the other states that all wavelengths across the spectrum are emitted and our eyes perceive it as white (like the Sun).

Both are possible, however, this does not explain the lack of purple stars.

Answer 1

If the star is hot enough to peak at purple (about 420nm, about 7,000K), it will still look blue because the width of the emitted spectrum is large. There is no way to get black body radiation that looks purple to a human. The spectrum is not narrow enough, nor can it combine red and blue without peaking at yellow.

Elaboration of the above:

First, notice that the perception of color is a biological problem: it depends on the specific filters (what is relevant is mainly the peak wavelength and width of the spectrum to which they are sensitive to activation) which are in the retina (cones) and react to light. The perceived color depends in an indirect way to the pattern of activation of these three filters. To perceive purple, you need the light spectrum to be mostly within the range of about 380 to 450 nanometers, or some combination of more or less pure red and blue. If the spectrum also contains longer wavelengths, then the purple will start to degrade. The black body radiation follows Planck's law, and if it peaks at 420nm (center of purple), its width is large enough to degrade the perception of purple, see graph (a). Even if you raise the temperature to shift the curve to the left, the activation in the purple range will not be pure enough.

Second, if you wanted to specifically mix the same amount of blue and red, the distribution will correspond to that of about 5000K peaking at about green, but still wide enough to look yellow because of the spectrum width.

But remember, the perceived color depends on the spectrum shape in a complex way due to biology, not physics, and the black body radiation does not have a good spectrum shape for this to be possible. For more details you need to go deeper into color science.

Answer 2

Stars (unless they are cold enough, like in Fraxinus' answer), emit light nearly as blackbodies with a mixture of different wavelengths given by the Planck radiation law. One effect of this is that a star with a higher temperature will emit more radiation at every wavelength than a cooler star: even if the peak is far into the violet or ultraviolet region there is also more light in all the other colours.

However, this is not enough to rule out purple stars since one might imagine a star with way more violet light than the other wavelength looking purple. To actually check one needs to combine the Planck law with a colour model that tells us what the spectrum looks like to a human eye. This has been done, producing the "Planckian locus": the curve blackbodies follows in colour-space. This curve starts near red, and then progresses roughly as expected. At the hot end it turns blue, but as temperature goes to infinity it slows down and approaches a blue colour (in practice we would experience it as blinding white). It curves around so it never gets close to purple.

To get a purple-looking star you need something filtering out a lot of the long wavelengths. But that is not part of the standard behaviour of hot stars.

Answer 3

https://en.m.wikipedia.org/wiki/Brown_dwarf

Purple is somewhat ill-defined in terms of spectrum, but the wiki article above lists magenta as a possible visible color for brown dwarf stars.

Such a spectrum is formed in the chromosphere layer where the original blackbody-ish radiation is depleted of wavelengths belonging to the middle of the visible band.

Answer 4

Note: This is a new and improved answer. I will delete my old answer soon.

Colorimetry

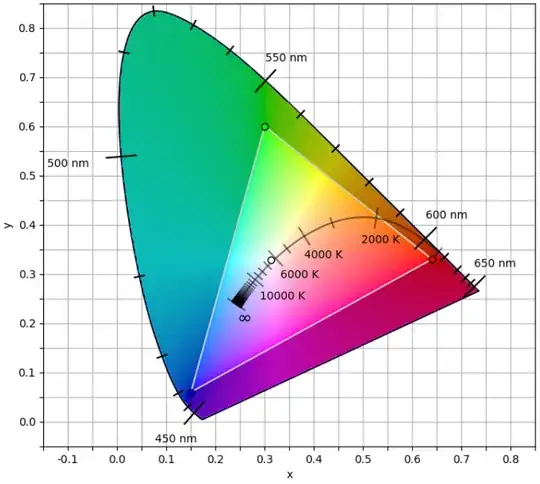
This figure is the xy chromaticity diagram form the CIE 1931 color space. The way we quantify color (colorimetry) is as follows. Light entering a sensor (e.g. the human eye) can be decomposed into a spectrum which gives the EM field intensity as a function of frequency or wavelength. The spectrum is a real-valued function $S(\lambda)$. We can use the xy chromaticity diagram to figure out what color this light will produce as follows. We define \begin{align*} X =& \int S(\lambda)\bar{X}(\lambda) d\lambda\\ Y =& \int S(\lambda)\bar{Y}(\lambda) d\lambda\\ Z =& \int S(\lambda)\bar{Z}(\lambda) d\lambda \end{align*} where $\bar{X}$, $\bar{Y}$ and $\bar{Z}$ are the "CIE XYZ standard observer color matching functions" seen below.

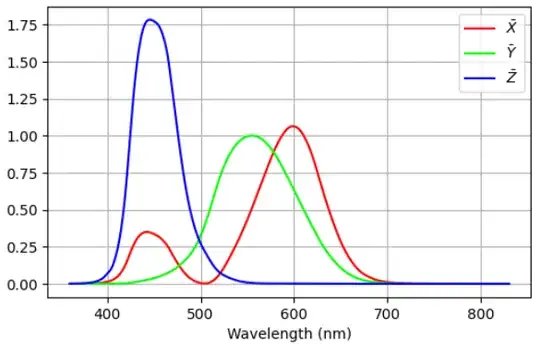
Note that $\bar{X}$, $\bar{Y}$ and $\bar{Z}$ are related to, and can be derived from the sensitivity of the L-, M-, and S-type cone sensors in the human eye captured in the LMS color space. However, the XYZ color space is different than the LMS color space.

For the given spectrum $S(\lambda)$ we calculate $X$, $Y$, and $Z$ and then from these we calculate \begin{align*} x =& \frac{X}{X+Y+Z}\\ y =& \frac{Y}{X+Y+Z}. \end{align*} The tuple $(x, y, Y)$ then identifies a unique sensation of color. $x$ and $y$ specify a chromaticity (e.g. a hue) on the xy chromaticity diagram and $Y$ specifies a brightness. $(x, y)$ values outside of the colored shape in the diagram are non-physical. No physical spectrum $S(\lambda)$ would lead to values $x$ and $y$ outside of this shape. This shape is called the visible gamut.

Note that it is possible for two different spectra $S_1(\lambda)$ and $S_2(\lambda)$ to produce the same values for $(x, y, Y)$. In this case a human will have the same color sensation. Two such spectra would be called metamers.

The diagram above is colored as follows. Focus first on the triangle in the center. This is the sRGB gamut. This is a set of colors that can be produced on most screens and monitors. Inside of this triangle each $(x, y)$ chromaticity is displayed with the maximum value of $Y$ the can be displayed in the sRGB color space. This is limited by the maximum brightness of the red/green/blue pixels in an (idealizied) sRGB display. Outside of that triangle it is impossible to produce those chromaticities on an sRGB display. In the diagram above if you draw a ray from the white point in the center to some point outside the sRGB gamut but still in the visible gamut then the point outside the gamut is colored with the same color as where the ray intersects the sRGB triangle, just with a darker color to emphasize it is a crude interpolation rather than the actual chromaticity that should appear at that point in the diagram..

The most important thing from this section is to understand that we can convert any spectrum to a color specified as an $(x, y)$ point in the chromaticity diagram. If a spectrum $S(\lambda)$ has more weight at a given wavelength, then the $(x, y)$ point corresponding to the spectrum will be pulled towards that wavelength on the border of the chromaticity diagram.

The Color of Monochromatic Light

Look at the xy-chromaticity diagram. If you look at the upper edge you can see color versus wavelength for monochromatic light. (Note that this story is distorted by the fact that monochromatic light is always outside the sRGB gamut, so what is displayed on your screen is an approximation to the color of monochromatic light). We can plot this directly. 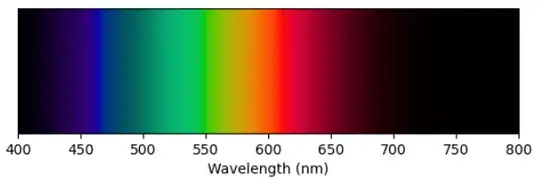Here the chromaticity displayed is derived using the interpolation described above for chromaticities outside the sRGB gamut. The brightness comes directly from $\bar{Y}(\lambda)$ plotted above.

This figure is an approximation to how monochromatic light of constant intensity looks at different wavelengths. Note that no monochromatic light produces a sensation of "purple". Short wavelengths look blue and long wavelengths look red. In between there is green and some yellow. I believe the bright streak in the blue data is an artifact due to inaccuracies in the datasets used to derive the CIE XYZ color space in the blue region of the spectrum but I am not certain (see https://en.wikipedia.org/wiki/CIE_1931_color_space#Subsequent_refinements).

By looking at the chromaticity diagram we can see that to create purple you need blue light and red light, but not green light. If there is green light then you can see the $(x, y)$ point will be pulled away from the purple region of the chromaticity diagram.

Blackbody spectra and color

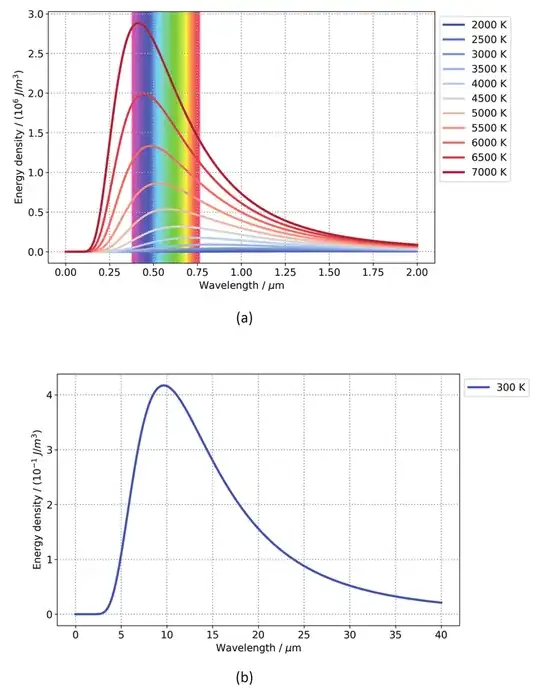
A blackbody emits radiation with a spectrum given by

$$ S(\lambda) = \frac{2hc^2}{\lambda^5} \frac{1}{e^{hc/\lambda k_B T} - 1} $$ We plot this below

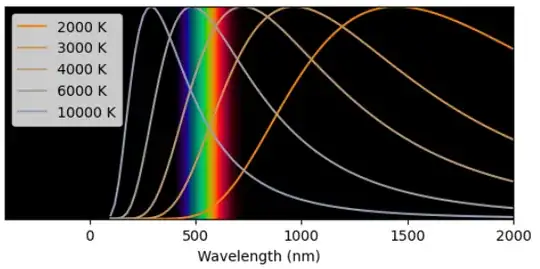
The blackbody spectrum is plotted for different temperatures. The corresponding traces are colored according to the color that that spectrum would appear (all traces shown at the Y=0.35). The visible color spectrum is shown in the background for reference.

We see a few important features. First, in the temperature ranges where the frequency spectrum overlaps with the visible spectrum, the spectrum is always as wide or wider than the visible spectrum (this is not a coincidence, it is not surprising that our eyes developed sensitivity in a the same optical band which is emitted by our local star at ~5500 K). Since the spectrum is so wide we shouldn't expect a single color to be "picked out" by a blackbody spectrum. Rather, we expect to see an even combination of colors (white) or perhaps white but tinted towards red or towards blue.

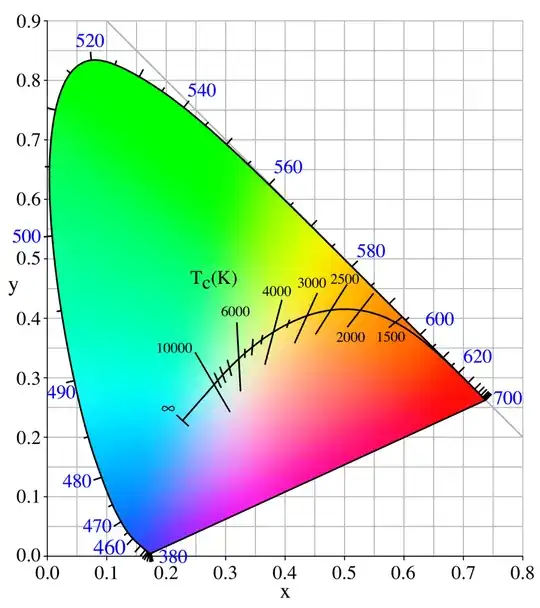
We can calculate and plot the color for different temperatures. 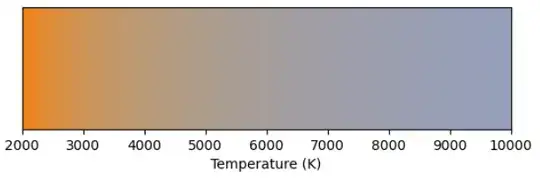These are shown at constant $Y=0.35$ which is the brightest $Y$ we can use to show all these colors with uniform brightness within sRGB. These colors are also indicated on the xy chromaticity diagram above.

All of these different analyses and visualizations lead to the same conclusion: Because the blackbody spectra are so broad, you can only get white light that is slightly tinted red or blue. As has been said, to get purple light you would need something to cut the green out of the spectrum.

This has been a thorough answer as to why blackbodies will not appear purple. So, if you accept that stars are blackbodies, you should now understand why there are no purple stars.