Let me rephrase the question:
I have a spectrum $S(\lambda)$. How do I reproduce the chromaticity (color) and brightness of this spectrum on an sRGB compatible screen?
I am going to answer this question with a specific focus on getting the brightness correct.
Radiometric Units
The question says that we have a spectrum $S(\lambda)$.
What does this mean? Suppose we have some light emitting object. We know that light carries energy. We could put the light emitting object in a calorimeter and measure, in a certain time $T$, how much energy was released as light. This is called the radiant energy emitted by the object. If we calculate the energy radiated per unit time then we have calculated the radiant flux. However, we might notice that the object emits more in some direction than another. We can then calculate, per unit steradian, how much radiant flux goes in any direction. This gives us the radiant intensity. We also might notice that the object is extended and different parts of it have more or less radiant intensity. Calculating radiant intensity per surface area of the object gives us the radiance. Finally, we may notice that the radiant intensity is not evenly distributed across wavelengths. Calculating the radiant intensity per unit wavelength gives us the spectral radiance. We can summarize these radiometric quantities and their representative units.
- Radiant energy: total electromagnetic energy radiated by the object: J
- Radiant flux: electromagnetic energy radiated per unit time: W = J/s
- Radiant intensity: Radiant flux emitted per unit steradian: W/sr
- Radiance: Radiant intensity per unit surface area of the emitter: W/sr/$\text{m}^2$
- Spectral radiance: Radiance per unit wavelength: W/sr/$\text{m}^2/\text{m}$
We can imagine a physical measurement using an optical spectrum analzyer to measure the radiant intensity emitted by different parts of an object into different directions as a function of wavelength to measure the spectral radiance of the object. We might then say we have measured
\begin{align*}
S_R(\lambda, t, \theta, \phi, x, y)
\end{align*}
Where $S_R$ has units of W/sr/$\text{m}^3$, $\lambda$ is the wavelength, $t$ is the time, $\theta$ and $\phi$ specify a direction and $x$ and $y$ specify coordinates on the objects surface. For our purposes we will only consider $S$ for specific values of $t$, $\theta$, $\phi$, $x$ and $y$ so that we can just write
$$
S(\lambda) = S_R(\lambda).
$$
Photometric Units
However, this problem involves the visual perception of light. An alternative system of units has been developed which rescale the above quantities by the photopic luminous efficiency function which captures the sensitivity of the human eye under well-lit conditions to different wavelengths. The luminous efficiency function will be specified by the dimensionless $\bar{Y}(\lambda)$.
We can then define the spectral luminous as
$$
S_L(\lambda) = K\bar{Y}(\lambda)S_R(\lambda)
$$
where $K$ is a constant having the value
\begin{align*}
K = 683.002 \frac{\text{cd}}{W/sr}
\end{align*}
This constant is related to the SI definition of the candela.
We see that the spectral luminance has units of cd/$\text{m}^2/\text{m}$
The luminous efficiency function $\bar{Y}(\lambda)$ can be found here and looks like
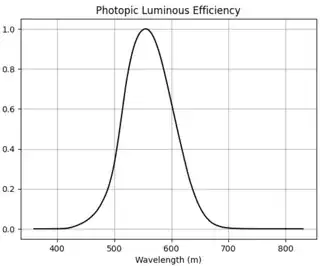
So we see that if we have the same radiant intensity at 550 nm and 650 nm, the radiant intensity at 550 nm will appear much brighter.
If we integrate the spectral luminance over all wavelengths we get the object's luminance with units of cd/$\text{m}^2$. If we integrate of the surface of the object we get the object's luminous intensity with units of cd. If we integrate over solid angles we get the object's luminous flux with units of $\text{cd}\cdot \text{sr} = lm$, lumens. If we integrate over time we get the luminous energy emitted with units of $lm\cdot s$. We can summarize the photometric counterparts to the radiometric units.
- Luminous energy: total luminous energy radiated by the object: $\text{lm}\cdot s$
- Luminous flux: luminous energy radiated per second: lm
- Luminous intensity: luminous flux radiated per unit steradian: lm/sr = cd
- Luminance: luminous intensity radiated per unit surface area of the emitter: cd/$\text{m}^2$=nit
- Spectral luminance: luminance per unit wavelength: cd/$\text{m}^2/\text{m}$=nit/m
The cd unit was defined so that the luminous intensity of a candle is about 1 cd.
I've introduced the nit=cd/$\text{m}^2$ unit which is a measure of luminance and is used to quantify, e.g. monitor brightness. We will see that the sRGB standard specifies a standard luminance of 80 nits. However, I did a search for some gaming monitors and saw that all monitors specify at least 200 nits, and one monitor specified up to 1000 nits.
We can always convert from a radiometric quantity to its corresponding photometric quantity by integrating the spectral version of the radiometric quantity against the luminous efficiency function and multiplying by $K$. For example, the luminance is calculated by integrating the spectral luminance which is equal to the product of the luminous efficiency function and the spectral radiance:
$$
L = \int S_L(\lambda)d\lambda = K\int S_R(\lambda)\bar{Y}(\lambda) d\lambda
$$
XYZ Color Space
The next part of the answer involves representing $S(\lambda)$ in different color spaces. The idea of color spaces is motivated by the observation that we can mix different combinations of colors but have the same perceptual experience of color and brightness. The phenomenon that different spectra can result in the same perceptual experience is called metamerism. The question is if we can apply some transformation to $S(\lambda)$ such that if two objects have the same transformed values then humans will have the same perceptual experience when observing the two spectra.
This question was studied in the early 20th century and resulted in the introduction of the 1931 CIE XYZ color space. We apply the following transformation to the spectrum $S(\lambda)$ to realize its representation in the XYZ color space:
\begin{align*}
X =& \int S(\lambda) \bar{X}(\lambda)d\lambda\\
Y =& \int S(\lambda) \bar{Y}(\lambda)d\lambda\\
Z =& \int S(\lambda) \bar{Z}(\lambda)d\lambda
\end{align*}
where the functions $\bar{X}$, $\bar{Y}$ and $\bar{Z}$ are the dimensionless CIE XYZ standard observe color matching functions which can be downloaded here and look like
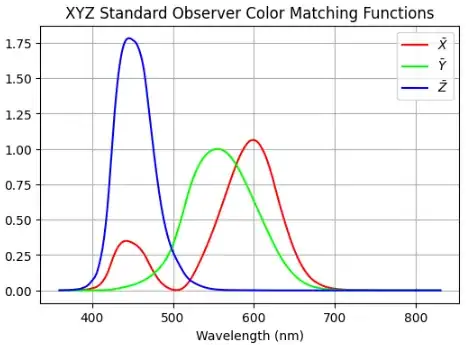
These color functions were experimentally determined using human subjects and color matching apparatus. The color matching apparatus allows researchers to understand and quantify how light with different spectra could result in the same perceptual experience for the human subjects.
Note the units of $X$, $Y$ and $Z$. If $S(\lambda)$ is the spectral radiance then $X$, $Y$, and $Z$ will all have units of radiance. It is very important to note that the $\bar{Y}$ function was chosen to exactly match the photopic luminous efficiency function. This means that $KY$ is equal to the luminance of the light source.
The RGB Color Space
The primary purpose of the XYZ space is to solve the problem of answering when two spectra will result in the same perceptual experience for human observers. The primary purpose of the RGB color space, by contrast, is generate spectra which will produce certain perceptual experiences for human observers.
It had been observed that the combination of varying amounts of red, green, and blue colored light sources allowed for the possibility to generate a wide range of color perceptions. The RGB and sRGB color spaces formalize this idea, especially with the idea of using arrays of pixels with red, green and blue lights to create screens for the viewing of colored text and images.
The RGB specification supposes that we have three light sources labeled "red", "blue", and "green" and with spectral radiances $S_R$, $S_G$, and $S_B$. Suppose also that each light source can be tuned from 0 total radiance up to some maximum radiance. We can then realize any spectrum
$$
S_{RGB} = RS_R(\lambda) + GS_G(\lambda) + BS_B(\lambda)
$$
for $0 \le R, G, B \le 1$.
The spectra $S_R(\lambda)$, $S_G(\lambda)$ and $S_B(\lambda)$ should satisfy, for all values $(R, G, B)$ between 0 and 1 the following matrix equation:
\begin{align*}
\begin{pmatrix}
X\\Y\\Z
\end{pmatrix}
= &
C\begin{pmatrix}
0.4124 & 0.3576 & 0.1805\\
0.2126 & 0.7152 & 0.0722\\
0.0193 & 0.1192 & 0.9505
\end{pmatrix}
\begin{pmatrix}
R\\G\\B
\end{pmatrix}\\
\boldsymbol{v}_{XYZ} =& C \boldsymbol{M}\boldsymbol{v}_{RGB}
\end{align*}
Where the $(X, Y, Z)$ vector on the left is the XYZ color space representation of the spectrum $S_{RGB}(\lambda)$ for the $(R, G, B)$ values in the vector on the right. Recall that $(X, Y, Z)$ have dimensions of radiance whereas $(R, G, B)$ are dimensionless. The constant $C$ therefore must have dimensions of radiance.
Let us multiply both sides of this equation by $K$ and look at the equation in the second row for $(R, G, B) = (1, 1, 1)$
$$
KY = KC(0.2126 + 0.7152 + 0.0722) = KC
$$
We see that the left side is the luminance of the $S_{RGB}(\lambda)$ spectrum and the right hand side is the constant $KC$. So we see that $KC$ should be equal to the maximum luminance of the RGB device realized when all three lights are turned to the maximum radiances. For example, if a screen has a maximum luminance of 200 nits then
\begin{align*}
KC =& 200 \text{ nit}\\
C =& 200 \text{ nit}/K = 200 \text{ nit} \times 0.00146 \frac{\text{W}/\text{sr}}{\text{cd}} = 0.293 \text{ W/sr/}\text{m}^2
\end{align*}
The sRGB color space
The sRGB color space is related by a simple non-linear transformation to the RGB color space.
\begin{align*}
sR =& \Gamma(R)\\
sG =& \Gamma(G)\\
sB =& \Gamma(B)
\end{align*}
where the $\Gamma$ function is given by
$$
u = \Gamma(v) = \begin{cases}
Av &\text{ for } v \le V\\
(1+c)v^{1/\gamma} - c &\text{ for } v > V
\end{cases}
$$
and its inverse is
$$
v = \Gamma^{-1}(u) = \begin{cases}
u/A &\text{ for } u \le U\\
\left(\frac{u+c}{1+c}\right)^\gamma &\text{ for } u > U
\end{cases}
$$
with $U=0.04045$, $V=0.0031308$, $A=12.92$, $c=0.055$ and $\gamma=2.4$. It seems that the sRGB color space arose out of a desire to save a data storage problem. On computers the RGB values must be each be stored using a certain number of bits. They are traditionally stored using 8 bits, or 2 bytes, each. This is why you sometimes see RGB values specified between 0-255 or as hexadecimal values between #00 and #FF. However, it was observed that over some ranges changing the binary value by one digit resulted in a small perceptual changes but over other range the same single digit change resulted in a large perceptual change. The idea of the gamma function is to resample the RGB space in such a way that changing by one digit results in the same perceptual change across the entire range. This means that you won't waste storage space tracking differences that humans can't perceive and you will also have a finer chromatic resolution where humans can more easily perceive differences.
Putting it all together
We can now specify exactly how to use an sRGB monitor to produce a spectrum $S'(\lambda)$ such that a human viewing the monitor will have the same perceptual experience as if they were viewing the spectrum $S(\lambda)$.
We first convert $S(\lambda)$ to the XYZ color space so that we have $(X, Y, Z)$. We then convert to the RGB color space using $\boldsymbol{M}^{-1}$:
\begin{align*}
\begin{pmatrix}R\\G\\B\end{pmatrix}
= \frac{1}{C}\boldsymbol{M}^{-1} \begin{pmatrix}X\\Y\\Z\end{pmatrix}
\end{align*}
where $\boldsymbol{M}$ is the matrix above and $C = L_{\text{max}}/K$ where $L_{\text{max}}$ is the maximum luminance of the screen.
Finally we calculate the sRGB colors
\begin{align*}
\begin{pmatrix}sR\\sG\\sB\end{pmatrix} = \begin{pmatrix}\Gamma(R)\\\Gamma(G)\\\Gamma(B)\end{pmatrix}
\end{align*}
These sRGB values can then be passed into a standard display software and, if the display is well calibrated to the sRGB standard, then the resulting color and brightness will match that of $S(\lambda)$.
What if the sRGB values are outside (0, 1)
If any of the sRGB values are below 0 then this means that it is impossible to represent that chromaticity using sRGB. In some sense it means you need something e.g. redder than the reddest red the screen can produce. The sRGB gamut is a subset of the entire visible gamut so there are just some colors that can't be produced by it. You can work around this by mapping the color in the visible gamut to the nearest representable color in the sRGB gamut. There are different ways to do this interpolation. I could go into greater detail on all of this, but that my be a topic for a separate question.
If any of the sRGB values are greater than 1 then this means your spectrum might live within the sRGB gamut, but your monitor is not bright enough to display it. One way to work around this is to convert your sRGB values back to RGB, divide all the values by the maximum value so that the new maximum value is 1, then convert back to sRGB. This procedure will retain the target chromaticity but will use the maximum brightness in lieu of the impossible requested brightness.
Monitor Settings
I am by no means an expert in color science, and color science is not a part of my work (though I do work with highly monochromatic lasers which has led to some of my interest). For some people, such as graphic designers or other types of visual artists, it is important that their monitors accurately reproduce the requested spectra. Everyone will be familiar with the brightness settings on monitors that at least change the $C$ parameter described above. However, there are even more settings for adjusting $\gamma$, color temperature and more. A manufacturer or professional can use calibration hardware and software to tune monitors for more accurate color reproduction. But the point I want to get across is that there are settings that will change the color produced for a monitor EVEN FOR THE SAME (sR, sG, sB) values. So the point is that the above discuss only holds accurately for a screen that has been well-calibrated to the sRGB standard.
Note also that the sRGB standard specifies the XYZ values for the red, green, and blue primaries used to generate the colors, but it does NOT specify the exact spectra they must have. So different manufacturers may choose different spectra. This should be ok as long as the correct XYZ values are realized. However, you can imagine that low quality engineer or manufacturing could result in primaries that do not hit the correct XYZ values. This would result in some distortion of the produced colors.
Another idea is that a monitor could have the possibility to display a LARGER gamut than sRGB (but still smaller than the full visible gamut). In that case the three sRGB values would no longer be directly proportional to the brightnesses of the three primary colors. In this case you would either need to use a different conversion matrix $\boldsymbol{M}$ or do some additional transformations so that the sRGB values in a software program produce the correct spectral output. But, of course, to realize colors outside the sRGB spectrum you will need to use a framework outside of the sRGB standard. This is all getting far outside of things I know about.

