Two-level system and a classical oscillator - energy

Question

I have solved two related problems and have some questions about the results.

1. Forced classical oscillator with the following equation:

$$\ddot{x}+\omega_{0}^{2}x=\varepsilon e^{-\gamma t}\sin\omega t,\qquad x\left(0\right)=0,\qquad\dot{x}\left(0\right)=0.$$

2. Quantum two-state system, derived from harmonic oscillator 0 and 1 states with the same force acting as a perturbation:

$$\left[\begin{array}{c} \dot{C}_{1}\\ \dot{C}_{2} \end{array}\right]=-ie^{-\gamma t}\sin\omega t\left[\begin{array}{cc} 0 & \Omega e^{-i\omega_{0}t}\\ \Omega e^{i\omega_{0}t} & 0 \end{array}\right]\left[\begin{array}{c} C_{1}\\ C_{2} \end{array}\right],$$

$$\Psi = C_1 \psi_0 + C_2 \psi_1,\qquad C_1(0)=1,\qquad C_2(0)=0,$$

$$\hbar \omega_0 = E_1-E_0,\qquad \Omega=\frac{m\varepsilon}{\hbar}\left\langle \psi_{0}\right|x\left|\psi_{1}\right\rangle = \sqrt {\frac{m\varepsilon^{2}}{2\hbar\omega_{0}}}. $$

The exact solutions are long, so instead I'll show approximate results for the quantity I was interested in.

The total energy transferred to the system from time $t=0$ to time $t\to +\infty$ under the condition $|\omega-\omega_0| \ll \omega_0$ and $\gamma \ll \omega_0$.

$$E_{cl}=\lim_{t \to \infty} \left(\frac{m\dot{x}^2}{2}+\frac{m \omega_0^2 x^2}{2} \right) = \frac{m\varepsilon^{2}}{8\left[\left(\omega-\omega_{0}\right)^{2}+\gamma^{2}\right]}$$

$$E_{q} = \lim_{t \to \infty} \hbar \omega_0 \left|C_2 \right|^2=\frac{\Omega^{2}\hbar\omega_{0}}{4\left[\left(\omega-\omega_{0}\right)^{2}+\gamma^{2}\right]}= \frac{m\varepsilon^{2}}{8\left[\left(\omega-\omega_{0}\right)^{2}+\gamma^{2}\right]}$$

In other words, I obtained exactly the same result, under the assumptions stated above.

What I wanted to ask, does this make sense physically? I know that two level system is kind of the quantum version of a simple oscillator, or we could even say that I was solving the actual quantum harmonic oscillator, but only restricted myself to two levels because of the resonance condition. Still, it was surprising to me that I obtained the exact same formula.

I'm also going to compare the exact solutions, but the quantum case is very hard to solve exactly.

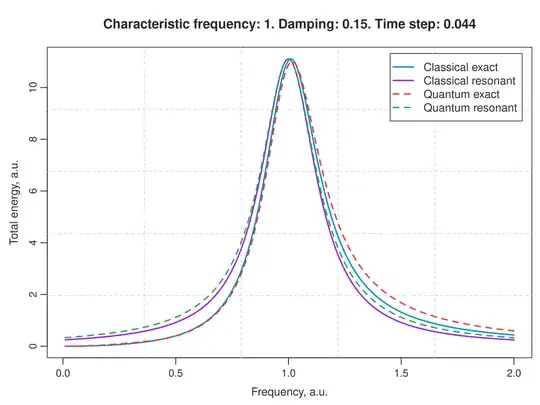
Edit: I did some numerical calculations. For the quantum two-level system the $E(\omega)$ dependence looks very similar to the classical oscillator, but not the same.

"Resonant" means the approximation $|\omega-\omega_0|\ll\omega_0$ in both cases. The time step seems large, but I used an implicit 4th order scheme, so it's pretty accurate. Just to clarify, I used numerical integration for the two-level system, both exact and approximate. For classical system I used the actual exact solution.

Answer 1

I already started to answer in comments, but I'll add some details here, about my reasoning. First, I think we should have some clarification about this problem using two tools: the Heisenberg picture and the Ehrenfest theorem. We could check, for example, in this nice Roger V. answer, that for a narrow wave packet, or an harmonic potential, we would have

$$ \frac{d}{dt}\langle x\rangle=\frac{\langle p\rangle}{m}, \frac{d}{dt}\langle p\rangle=-\frac{dV(\langle x\rangle)}{dx} $$

To include the effect of the external force, we should take into account the potential $V_{int}(x) = \epsilon x e^{-\omega t}\sin(\omega t)$. In general, we would include $\langle - \frac{d}{dx}V_{int}(x)\rangle$, but it will result in $ \epsilon e^{-\gamma t}\sin(\omega t)$ so

$$ \frac{d^2}{dt^2} \langle x\rangle +\omega_0^2\langle x\rangle = \epsilon e^{-\gamma t}\sin (\omega t). $$

For the state $\psi_0$, $\langle x\rangle = 0$ and $\frac{d}{dt} \langle x\rangle = 0$, so we have the same problem as your classical case, but for the variable $\langle x\rangle$.

Now, solved this problem, we can calculate the mean energy. We have the quantum Hamiltonian

$$ \mathcal H = \frac{1}{2m}p^2 + \frac 12 m\omega_0^2 x^2 + V_{int}(x) $$

So $E_{q} = \langle \mathcal H\rangle$. The unperturbed part is easy, since it is quadratic. For the interaction part, the quantity will match the classical case if we can guarantee that $\langle V_{int}(x)\rangle = V_{int}(\langle x\rangle)$. But this potential is linear in $x$, so the condition is always fulfilled. The conclusion is that the mean energy should match the classical case.