Background: Ashcroft and Mermin provide a discussion in Chapter 14 describing de Haas-van Alphen oscillations and their use in measuring the Fermi surface of a material. In doing so, they present the expression $\Delta \biggl( \frac{1}{H} \biggr) = \frac{2\pi e}{\hbar c}\frac{1}{A_e}$ where $A_e$ is an extremal cross-sectional area of the Fermi surface in a plane normal to the magnetic field and $\Delta \biggl( \frac{1}{H} \biggr)$ is the change in $\frac{1}{H}$ through a "single period of oscillation". It is often said that these oscillations can be used to determine the Fermi surface of a material (e.g. in A&M Ch. 14 and on the wikipedia page for dHvA.
Question: My question is how can we use this formula to map out the Fermi surface? Consider a concrete example of the de Haas-van Alphen oscillations for silver:
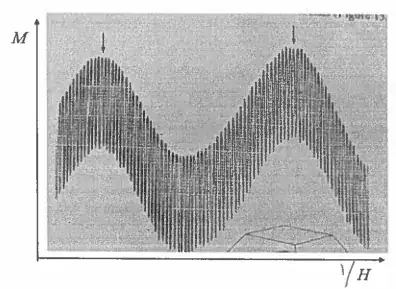
What exactly can be said about the Fermi surface from these oscillations?