First, note that when we discuss "observers" here we really mean inertial frames of reference. These can never be defined by any single observer.
So, thinking visually about this, let's first imagine several observers, all equidistant from one another, moving with velocity $v$. I'm taking $c=1$ in the diagrams here, because it makes them simpler to understand: 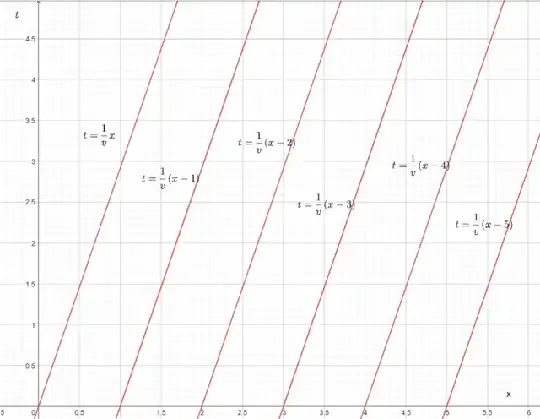
Let these observers be the representatives of the moving reference frame, that is, they are moving with respect to the frame where the boxes are stationary.
Now let us consider, how they may synchronize their clocks. We employ a very simple procedure. Take the observer corresponding to the worldline $t=\frac{1}{v}(x-3)$, and have him at a certain moment send light rays to his front and to his back directions together:
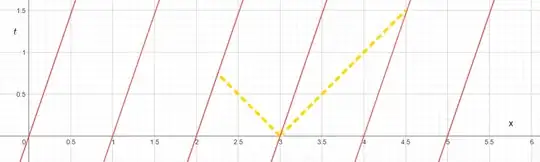
Now, the observers that are shown as getting the light signal, must agree to set their clocks to the same time, which is some $t_0'$, because they know this light signal came from an observer that is at all times an equal distance from both of them.
By this, we can already define one line on which we postulate every event must be simultaneous for the moving frame:
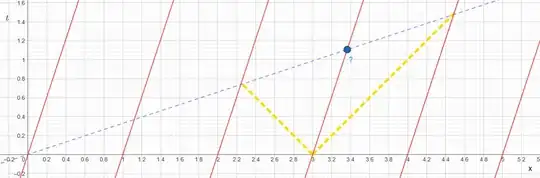
So we want to say this purple dashed line is indeed a line passing through all events that are measured to occur at a single instant $t_0'$, in the frame that's moving relative to the boxes.
But it's not clear yet, why for example the point indicated by $?$ in the diagram should also be assigned the same time $t_0'$ to which we said both indicated observers set their clocks.
It's a good exercise then to show, that if we compute the coordinates of that point and work where a light signal would have arrived from if we traced it "backwards", we would have found the following result (only visually shown here, not computationally):
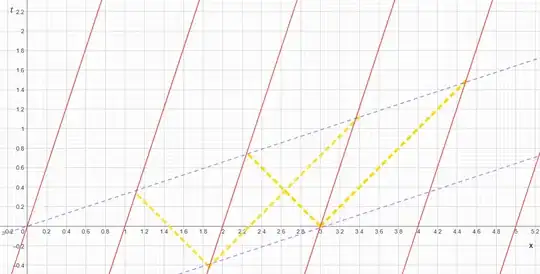
What we see is that it is precisely correct that if both observers corresponding to $t=\frac{1}{v}(x-2)$ and $t=\frac{1}{v}(x-3)$ sent a light signal in the same manner at the same instant where that instant is exactly defined by a line with the same slope as we found before, it would get to the observer in front and to the back of them at the same instant which is again defined by a line of identical slope.
To summarize this part, we see that the way we have identified the lines of simultaneity of the inertial frame that's moving relative to the boxes, is consistent with how the observers in this frame can ensure that all of their clocks are synchronized, and we have verified that these lines of simultaneity have a specific slope, that we have managed to identify via the above procedure.
Now, we're ready to talk about the exploding boxes. In the rest frame of the boxes the situation is simple:
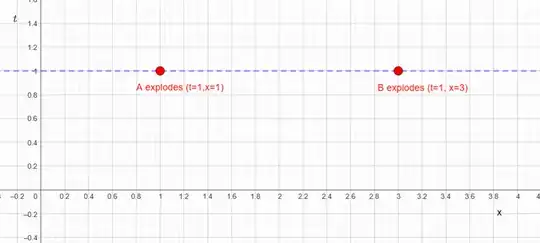
I've taken here that both explosions occur at the same instant in their rest frame, corresponding to coordinate time $t=1$. In this frame, box $A$ is stationary at $x=1$, and box $B$ is stationary at $x=3$.
How will the moving frame measure these events?
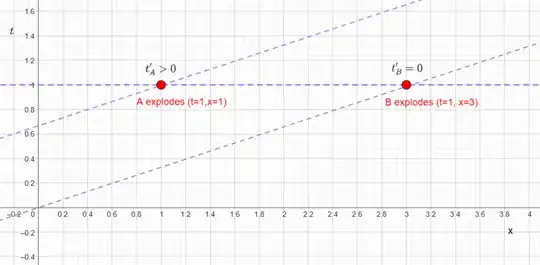
After the work done above, we immediately see that the line of simultaneity corresponding to box $B$ exploding, which is farther from the origin, is $t'=0$, which precedes the line of simultaneity corresponding to box $A$ which is closer to the origin, which is some $t'$ such that $t'>0$. Hence we see the moving frame assigns a later time to the explosion of box $A$ which is closer to the origin.
Why do we assert that box $B$ exploded at $t'=0$? Because by assumption here we take that both frames agree on their origin, in other words the event in the boxes frame $(t,x)=(0,0)$ is defined such that it has the same coordinates in the relatively moving frame $(t',x')=(0,0)$, which can also be verified via the Lorentz transformations.
Again for emphasis, being closer/farther from the origin is not the same thing as considering which things are closer or farther from any single observer. Frames are always taken to be composed of many (infinite, in fact) observers, all carrying synchronous clocks and having their assigned positions relative to an agreed origin. If you replace the word "frame" with "observer", you must keep in mind that it is only an "observer" in the sense of someone who has access to all this data, but in practice, this data can only be collected by stationing actual observers or measuring instruments all across space.
Because you've asked for an intuition, I've focused on visual arguments via the above spacetime diagrams and almost completely avoided relating the above to the Lorentz transformations. I highly recommend however that you connect this intuitive picture to the Lorentz transformations.
A good starting point will be noting that the lines of simultaneity in the frame that's moving relative to the boxes, are indeed given by:
$$ t'_0 = \gamma(t-vx) \Longrightarrow t=vx+\frac{t'_0}{\gamma} $$
Thus the slopes of the lines of simultaneity are precisely $v$ where again recall that we're working in units where $c=1$.
Note that interestingly, in this visual explanation we were able to derive the correct slope without any reference to the Lorentz transformation. That's because, as you can see, the $\gamma$ factor only comes in as a "calibration" factor, relating the rate of passage of time in both frames. Thus note that from the above procedure alone, we cannot deduce both $t_0'$ and $\gamma$ but only their ratio. To find the relative rate of passage of time in the moving frame, we need the full Lorentz transformation, the derivation of which requires several more assumptions than just the ones we made in the above clock synchronization procedure.
(All of the above diagrams were created via Geogebra).





