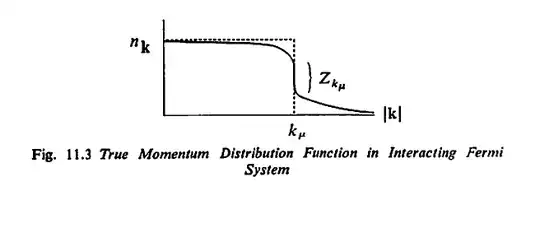
Why is a sharp discontinuity necessary to define the Fermi surface in interacting fermion systems?
Mathematically, if the Fermi surface were not sharp, it wouldn't be a surface. In other words, Fermi surface is an $(d-1)$-dimensional manifold in $d$-dimensional space of states, separating the filled states from the empty ones (at zero temperature.)
Fermi surface implicitly underlies our conventional understanding of material properties. Its absence is a manifestation of unusual properties.
The Fermi surface arises as a result of Fermi-Dirac statistics - at zero temperature all the states below this surface are fill, while all the states above it are empty. The excitations arise from transfer of particles from below Fermi surface to the vacancies above it.
Such behavior had important implications, some of which are:
- The excitations are fermionic, i.e., similar to classical particles - this ensures success of simple descriptions of material behavior, such as, e.g., Drude model (see Why do Drude/Sommerfeld models even work?). The success of Fermi liquid theory (for which the figure in the OP is) is in showing that excitations in many interacting electron systems are still particle-like, even with renormalized parameters. This is notably not the case in one dimension - Luttinger liquid has bosonic excitations and very different properties.
- There's no gap. The excitations can be created by moving particles with infinitesimally small energy from just below the Fermi surface to just above it. This implications for how conductance, specific heat and other properties behave like. An immediate example of a gapped material is superconductors, where inexistence of small energy excitations results in lossless current, and other peculiar behaviors.
Remark:
The important reason why the zero-temperature theory is so successful is that the values of Fermi energy in many materials are very high, ranging from tens to hundreds of Kelvin (in temperature units, where the Fermi energy is called Fermi temperature.) E.g., for iron we have $E_F=11.1$eV$=13\cdot 10^4$K. Thus, broadening of Fermi surface of the order of ambient temperature $T=300$K is often negligeable.
This is not the case in doped semiconductors used in industrial applications, where the Fermi energy is shallow. However, in semiconductor nanostructures, typically studied at Kelvin or milli-Kelvin temperatures, the metallic behavior is routinely present.
Related:
If a non-interacting particle behaves like an undamped wave, can an interacting particle behave like a damped wave?
Particle/hole excitations have finite lifetime