I don't quite understand why 2-loop pure graviton scattering is divergent. It looks UV finite to me when I naively compute the superficial divergence $$D=dL-2I\tag{1}$$ for $d=4, L=2, I=5$.
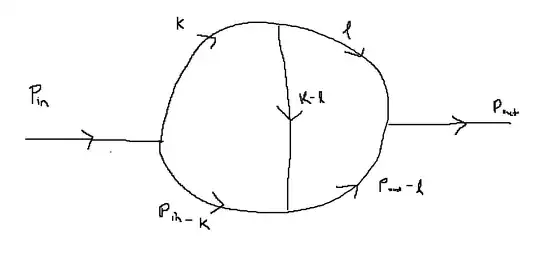
Consider the 1PI diagram built from 3-vertices below, we have $D=-2$
and the integral would look something like
$$\begin{equation} \int\frac{(d^4k)}{(2\pi)^4}\int\frac{(d^4l)}{(2\pi)^4}(-ig)^4\frac{i\mathcal{P}_{\mu\nu,\alpha\beta}}{k^2+i\epsilon}\frac{i\mathcal{P}_{\dots}}{l^2+i\epsilon}\frac{i\mathcal{P}_{\dots}}{(P_{in}-k)^2+i\epsilon}\frac{i\mathcal{P}_{\dots}}{(P_{out}-l)^2+i\epsilon}\frac{i\mathcal{P}_{\dots}}{(k-l)^2+i\epsilon}(2\pi)^4\delta^4(P_{in}-P_{out})\propto\int\frac{k^8}{k^{10}}=\Lambda^{-2} \end{equation}\tag{2}$$
where I am suppressing the indices structure with "$\dots$" for simplicity of typing the integral.
which is looks UV finite.
Am doing something wrong with my calculation? Where exactly do the UV divergences come from?