When I used to teach physics labs, I introduced frictional forces by attaching a force sensor to a block and then slowly and steadily applying more force until the block started to move, at which point I pulled it with constant speed. If I did my job properly, the result was a curve on the screen which looked like the following cartoon:
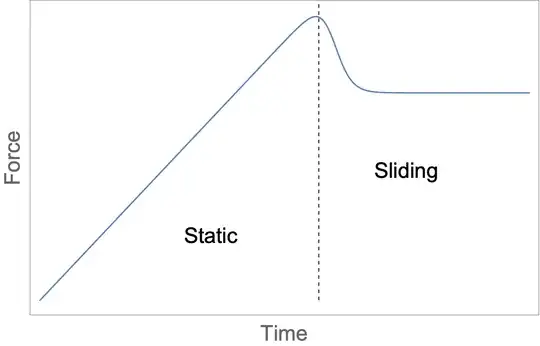
After doing this a few times with different objects, we would conclude that there are two regimes at play here. When the object isn't moving, friction would match whatever force I applied, up until a limit. Once that limit was reached, friction would exert a constant force. In that sense, there are two parameters - the maximum static friction force, and the value of the sliding friction force.
This would kick off the lab which was designed to test what factors influenced those two parameters. For a given pair of surfaces, students would observe that those two parameters are both roughly proportional to the normal force between the surfaces, with the conclusion being that
$$F_{s,max} = \mu_s F_N \qquad F_{k} = \mu_k F_N$$
where $mu_s$ and $\mu_k$ were coefficients which depended on the nature of the two surfaces in contact.
The fact that this "law" could be arrived at by undergraduates during a 3 hour lab should be an indication that it may be a dramatic oversimplification. That being said, it is a remarkably good approximation to reality, as long as you are willing to allow $\mu_s$ and $\mu_k$ to be empirical parameters which may change moment to moment. And really, as long as nothing dramatic is happening to the surfaces or in the environment, their values are surprisingly consistent trial to trial.
If we need to, we can always develop more sophisticated models - see e.g. this chapter of an online robotics textbook. To do this, we might apply our coarse approximation to a specific scenario and stress-test it to find its limitations and shortcomings, and then modify the model to make it more applicable. For example, in the cartoon above, we might enhance our model to quantiatively predict the shape of the transition between the static and sliding regimes.
Do these laws break down at some point? Yes. Are there surfaces and materials which are poorly described by these laws? Yes, certainly. But I love this model because it can easily demonstrate the heart of physics and empirical science in general. We observe a phenomenon, we develop a model for that phenomenon, we test the model, and we iterate until we can predict the outcomes of future experiments to our satisfaction. It doesn't matter if it's frictional forces or quantum field theory - when it comes down to it, this is what physics is.
