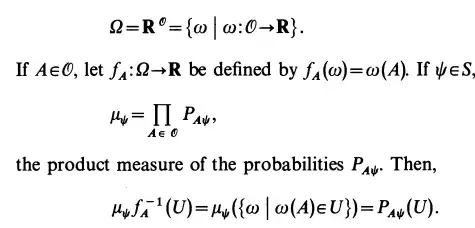Doubt regarding the trivial construction in the original Kochen-Specker article

Question

I'm trying to understand a construction in the first section of the original Kochen-Specker article (S. Kochen; E. P. Specker (1967). "The problem of hidden variables in quantum mechanics". Journal of Mathematics and Mechanics. 17 (1): 59–87. doi:10.1512/iumj.1968.17.17004. JSTOR 24902153.), my doubt is simply that two functions are said to be equal when their domains are quite different spaces.

First some context. In the original article of Koshen and Specker, before proving the theorem, they give a overview of what they mean by a Hidden Variable Theory. In their formulation, the first condition necessary for a hidden variable description of a given theory with observables $\mathcal{O} $ and states $\mathcal{S}$ is the following: If your theory allows you to predict the probability $P_{A\psi}(U)$ that the value obtained by the measure of an observable $A$, in the state $\psi$, falls in the interval $U\in \mathbb{R}$, then a Hidden Variable description is a state space $\Omega$ with functions $f_A:\Omega \rightarrow \mathbb{R} $, and a probability measure $\mu_{\psi}$ on $\Omega$ such that:

$$P_{A\psi}(U) = \mu_{\psi}(f_{A}^{-1}(U)) $$

This is condition (1). They then justify that this condition alone is insufficient, because it can always be satisfied, by offering a trivial construction satisfying condition (1). The construction is the following.

I understand the construction of the function $f_A$ but fail to see how the equality $$\mu_{\psi} = \Pi_{A\in \mathcal{O}}P_{A\psi}$$ can be a coherent definition for $\mu_{\psi}$. The probability measure takes as input sets of $\Omega$ while the fuction $P_{A\psi}$ takes as inputs sets of $\mathbb{R}$. The equality can only be true if $\Omega$ is homeomorphic to $\mathbb{R}$ somehow. Since no structure to $\Omega$ is mentioned I fail to see how this can be the case. Is the set of all functions from a set $\mathcal{O}$ to the reals homeomorphic to the reals themselves somehow? No structure on $\mathcal{O}$ is mentioned as well. My question is how do I make this make sense.

Answer 1

For any family of sets $(X_i)_{i\in I}$, $\prod_i X_i$ denotes the set of maps $f$ of domain $I$ such that for every $i$, $f(i)\in X_i$. In particular, $\prod_{i\in I} X$ is equal to the set of maps from $I$ to $X$, so is equal to the subset of $\mathcal{P}(I\times X)$ consisting on and only on subsets of $I \times X$ that are graphs of (everywhere-defined) functions.

Let us recall the following prerequisite from measure theory: if $(X_i)_{i\in I}$ is a family of measurable spaces, and if $(\mu_i)_{i\in I}$ is a family of probability measures, such that for each $i$, $\mu_i$ is a measure on $X_i$, then there is a unique probability measure on $\prod_i X_i$ such that for any subset of $\prod_i X_i$ of the form $\prod_{j\in J} B_j \times \prod_{i\not \in I} X_i$ for some finite subset $J$ of $I$ (of course, you have to keep the indices in the right order, I just wrote it like that for convenience), its measure is $\prod_{j\in J} \mu(B_j)$. This measure is called the product measure. See for example this wiki page and more generally any book on measure theory.

Here, $I=\mathcal{O}$, for every $A$, $X_A = \mathbb{R}$ and $\mu_A=P_{A\psi}$.