Although a huge amount of latent heat is released when steam condenses on an object, it can't condense faster than that energy can penetrate into the object, and that rate is limited by the object's internal thermal conductivity.
The object heats up until its surface temperature is just cool enough so that the equilibrium condensation rate provides energy at the same rate at which heat is conducted from the surface into the object.
Since an object's surface temperature ($\sim100$°C at sea level) and internal thermal conductivity are essentially the same whether the object is immersed in ambient-pressure steam or boiling water, we'd expect both pure steam and boiling water to roughly heat an ideal object at the same rate.
For real food and home cooking procedures, however, steaming is often slower because insulating air and water layers form on the food's surface that dramatically reduce the rate at which steam can transfer heat into the object.
Such layers are much less an issue for boiling, because they are removed by the boiling water which is much less gentle than steam.
Nathan Myhrvold summarizes this well in "Modernist Cuisine: The Art and Science of Cooking, Vol. 2"
Most cookbooks describe steaming as a much faster cooking method than boiling. Because steam can be hotter than the boiling point of water and can carry large amounts of latent heat energy, this makes intuitive sense even to those unfamiliar with the underlying physics. But in this case, intuition misleads.
… our experiments have shown that, in most situations in which steaming is used in the kitchen, boiling would be faster … The reason is that condensation actually slows down the cooking process rather than hastening it.
On surfaces that have any degree of roughness (i.e., nearly all foods), tiny droplets of condensation quickly combine to form a thin but uniform layer of water known as a film condensate. The film acts like a heat shield: it quickly cools to the temperature of the food it envelops, then dramatically reduces the ability of heat to flow from the steam into the food.
A second phenomenon slows the steaming of fruits and vegetables. In most produce, the tissue just beneath the surface is laced with pockets of moist air. Heat makes the air in these pockets expand and escape as the tissue collapses. Some of the expelled air gets trapped beneath the film condensate, creating a blanket of air between the food and the steam. The insulating properties of air surpass even those of water …. The result is that, for most produce, boiling is substantially faster than steaming.
Surface Heat Transfer Coefficient
How fast an object heats when immersed in a hot fluid depends on the heat transfer coefficient ($h$) between the fluid and the object's surface, the object's size (characteristic length scale $L$), and its internal thermal conductivity ($k$).
In terms of the dimensionless Biot number ($\mathrm{Bi}=hL/k$) that parameterizes the relative importance of heat transfer to conductivity, the overall heat transfer coefficient is
$$U \approx \frac{h}{1+\mathrm{Bi}} \longrightarrow \frac{k}{L} \qquad \mathrm{when}\ h\gg \frac{k}{L} $$
Food items typically have thermal conductivities in the range $0.1$ (e.g. a dry rice grain) to $0.6\,\mathrm{W/m/K}$ (e.g. broccoli), and size scales in the range $0.001$ to $0.05$ m, corresponding to Biot numbers in the range $10-10^2$ for boiling and $10^2-10^3$ for steaming (assuming ($h \sim 10^3\,\mathrm{W/m^2/K}$ for boiling and $\sim 10^4\,\mathrm{W/m^2/K}$ for steaming). This means we'd naively expect steaming to be $\sim0.1-10$% times faster than boiling, but this neglects the insulating effect of water/air/foam surface layers.
Effect of Surface Water Layer
When steam condenses on the surface of a food item, it creates a boundary layer of cooler liquid water, so subsequent steam is condensing on this water film. The steam is no longer directly heating the food, but is instead heating the water that in turn heats the food. So even when steaming, it is actually hot water that is heating the food. As long as boiling water convection or steam condensation keeps the water in direct contact with the food item's surface at $\sim100$°C, the food item should cook at the same rate in ambient-pressure steam or boiling water.
The thickness of the water layer depends on the surface topography, its smoothness, and on how hydrophilic or hydrophobic it is. The layer would keep building up except for absorption into the food and gravity causing the water to flow and drip off the bottom of the food item.
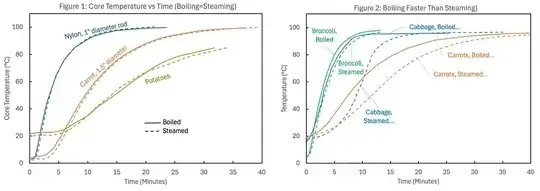
This is consistent with the heating curves shown in Figure 1 above, and also with simple thermal conduction models.
Thermal Conduction Models
Using well-known results dating back to Fourier (e.g. see Table 4-1 of Cengel 2007), the time evolution of the central temperature $T_{\mathrm{centre}}$ of a uniform infinite cylinder with initial internal temperature $T_{\mathrm{initial}}$, radius $r_0$, thermal conductivity $k$, specific heat capacity $c$, mass density $\rho$, and constant surface temperature $T_{\mathrm{surface}}$ is:
$$\frac{T_{\mathrm{centre}}-T_{\mathrm{initial}}}{T_{\mathrm{surface}}-T_{\mathrm{initial}}} = \sum_{n=1}^\infty\frac{2}{\lambda_n}\frac{J_1(\lambda_n)}{J_0^2(\lambda_n)+J_1^2(\lambda_n)} \ e^{\lambda_n^2 t/\tau_0}$$
where the time constant is $\tau_0=c \rho r_0^2/k$, $J_0$ and $J_1$ are Bessel functions, and the $\lambda_n$ are the roots of
$$\lambda_n\frac{J_1(\lambda_n)}{J_0(\lambda_n)}=\mathrm{Bi}$$
Values of thermal conductivities, heat capacities, and densities found online give $\tau_0 \sim 800-1200$ for nylon and $\sim 2500-3000$ seconds for carrots, and using the midpoints of these ranges give model curves that almost perfectly match the observed heating curves from Figure 1, as shown in Figure 1a below. We don't know the size of the potatoes used for the heating curve in Figure 1, but again taking online values for potato thermal properties, and the heating curve expected for spherical $6$ cm diameter potatoes is an excellent match to the observed data.
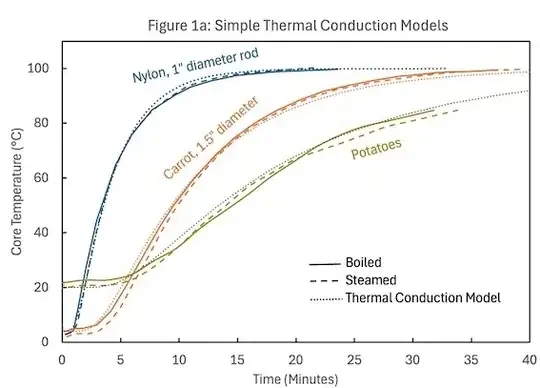
Effect of Air on Steam Heat Transfer
When a food item is placed in a steamer, it is unavoidable that large amounts of air are admitted, so at least initially there will be a significant fraction of air in the steam. As can be seen from the plot below (from Fig. 2.11 of Rocca-Poliméni 2007), even a tiny fraction of air mixed with the steams dramatically reduces the heat transfer rate.
This heat-transfer reduction is because when steam contains a non-condensable gas such as air, when the steam condenses on a surface, the uncondensed air accumulates at the liquid-vapour interface, creating an barrier that greatly reduces rate at which steam can heat the surface.
The air mixes with incoming steam, lowering its partial pressure and hence reducing its condensation temperature.
As little as $0.3$% air in steam can cut the heat transfer rate in half.
Insulating Foam Layer
Most food items contain air and watery juice that evolves from the item when heated. This is usually washed away in boiling water, but can form an insulating foam layer on the item's surface when heated by ambient steam. This can further reduce the heat transfer rate from the steam.
In principle, methods such as adding ultrasound to the steaming environment could reduce the foam layer, but this is not relevant for home cooking.
"Airy" Vegetables Take Longer to Steam
Given the effects of air & foam, it is unsurprising that steam is slower than boiling at heating less-solid vegetables such as broccoli and especially cabbage (as seen in Figure 2).
The difference between the carrots in Figures 1 & 2 implies that the thickness of any insulating layer can depend on how the food item is prepared.
In Figure 1, the carrot was a cylinder pre-soaked in ice water, while in Figure 2 the carrots were simply cut into cubes.
A simple thermal conduction model (not shown) using the same thermal parameters as for the carrot cylinder (in Figure 1) is an excellent fit to the boiled, but not the steamed, carrot cube heating curve in Figure 2.
The different preparations apparently resulted in the carrot cubes having greater average surface air-water content and/or surface permeability than the carrot cylinders, producing a much more significant surface insulation layer on the cubes that impeded the steam heating rate.
The variety of carrot, whether they are peeled or cut (exposing different tissues) and how fresh they are could all affect the steaming time.