I recently started studying general relativity and came across the following problem. Schwarzschild's solution is a solution to Einstein's equations in a vacuum, with a zero energy-momentum tensor. As far as I know, Schwarzschild did not consider any physical system (a star or a black hole) when he was looking for this solution, he was simply looking for a spherically symmetric solution (a purely mathematical problem). How did it happen that this solution describes a black hole? Is the energy-momentum tensor for a black hole equal to 0? Yes, it is equal to 0 where there is no mass, but the mass is concentrated somewhere. It seemed to me that in order to find a metric around a black hole, one should take the energy-momentum tensor equal to the delta function (in the sense that all the mass is at the origin, at one point). And then solve Einstein's equations with such an energy-momentum tensor (it will no longer be zero). For example, there is a problem of solving the Einstein equations for a spherically symmetric star, where the energy-momentum tensor will be equal to 0 at $r>R$ (radius of the star), but at $r<R$ it will be non-zero, depending on the density and pressure at the particular point (usually the ideal fluid model is used). From this problem one can get the Oppenheimer-Volkoff equation (https://en.wikipedia.org/wiki/Tolman%E2%80%93Oppenheimer%E2%80%93Volkoff_equation). And in this case, I understand the physical formulation of the problem, it is clear why the energy-momentum tensor is what it is. But for a black hole?
4 Answers
The Schwarzschild solution is not specifically for a black hole, although it does cover that. The Schwarzschild solution is a spherically symmetric vacuum solution. So it covers the vacuum region outside of any spherically symmetric distribution of matter. This includes ordinary (non-rotating) planets and stars. A black hole is just a limiting case of this spacetime as the areal radius of the outer surface goes to zero.
- 117,350
This is due to Birkhoff's theorem:
In general relativity, Birkhoff's theorem states that any spherically symmetric solution of the vacuum field equations must be static and asymptotically flat. This means that the exterior solution (i.e. the spacetime outside of a spherical, nonrotating, gravitating body) must be given by the Schwarzschild metric.
The point is that regardless of what the mass distribution of body is, as long as it is spherically symmetric outside the body the metric will be the Schwarzschild metric. Whether it's a star with a non-zero volume or a delta function mass at $r = 0$ makes no difference.
For completeness we should note that the Schwarzschild black hole does not have a delta mass at $r = 0$. In fact the point $r = 0$ is not part of the manifold at all. The mass in the Schwarzschild metric is a geometrical property called the ADM mass.
- 367,598
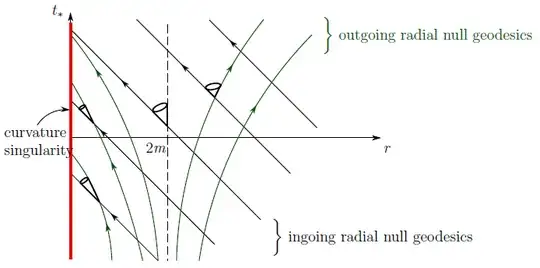
The Schwarzschild solution yields a region of spacetime which nothing inside it can escape outside it unless causality is broken. The geodesics just do not allow for that (see figure). The light cones past the event horizon are tilted in a way that gives you no way out. This is the definition of a black hole.
- 131
Lots of good answer, but everything I know about blackholes I learned from Kip Thorne, and since he's world famous, he's on YouTube$^{1, 2, 3}$.
He explains that a blackhole doesn't contain matter. The in-falling material crosses the horizon, and then the singularity is point in its future, when it is destroyed.
The singularity contains all the non-zero $G_{\mu, \nu}$ as a topological defect in space-time (it's not part of space-time anymore), and the Schwarzschild solution is the warped-space time that cloaks that and connects it back to asymptotic Minkowski space.
All the mass/energy of to progenitor star now resides in the warped space-time surrounding the singularity. (I note that Kip always says warped---because it's not flat, but as you pointed out: it's a vacuum solution with zero curvature (via the Einstein tensor).
[1] https://www.youtube.com/watch?v=oj1AfkPQa6M&list=PLFJr3pJl27pItxUFeZlx98GQzl-5UBroJ&index=10
[2] https://www.youtube.com/watch?v=tiocBE51yuc&list=PLFJr3pJl27pItxUFeZlx98GQzl-5UBroJ
[3] https://www.youtube.com/watch?v=ThuFewi-mRM&list=PLFJr3pJl27pItxUFeZlx98GQzl-5UBroJ&index=3
- 42,131