In this answer, I will first set up a number of necessary concepts. With those in place, I will discuss the dynamics in the section titled: 'The dynamics'.
I will then proceed to give a dynamical derivation of the acceleration relative to the rotating coordinate system.
To understand the east-west component, I recommend the approach of John Marshall and R. Alan Plumb.
It's a series of pages that accompanies a textbook on atmospheric and oceanic dynamics written by Marshall and Plumb.
As a conceptual model for the dynamics of buoyant mass in motion over the surface of the rotating Earth, they use a turntable with a surface having a parabolic cross-section. The turntable surface is very shallow. The construction is described on the page Construction of parabolic turntable
A disk with a rim, diameter of about a meter, is filled with a resin that will slowly set, and rotation of the disk is started at 10 revolutions per minute.
Due to the rotation, the still-fluid resin redistributes to a concave shape. The fluid's final state is referred to as 'solid body rotation'. The final state has the property that everywhere the slope of the surface provides the required centripetal force to remain in an overall co-rotating state.
Over the course of hours, the resin cures. The last step to prepare for demonstration is to sand the surface to a smooth finish.
About the resulting shape:
for sustained co-rotating motion, the required centripetal force is proportional to the square of angular velocity and in linear proportion to the radial distance. That is, twice the radial distance, twice the amount of centripetal force required.
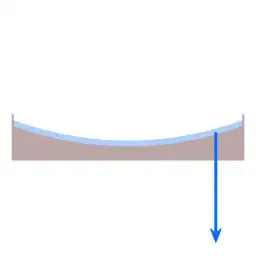
Forces on a parabolic dish
The image is an animated GIF consisting of three frames. The blue arrow represents gravity, while the red arrow represents the force of buoyancy. Note that the buoyancy force is always perpendicular to the local surface.
To demonstrate the motion of an object over that dish, a small disk of frozen carbon dioxide is released. The sublimating carbon dioxide creates a gas cushion so that the motion has very little friction.
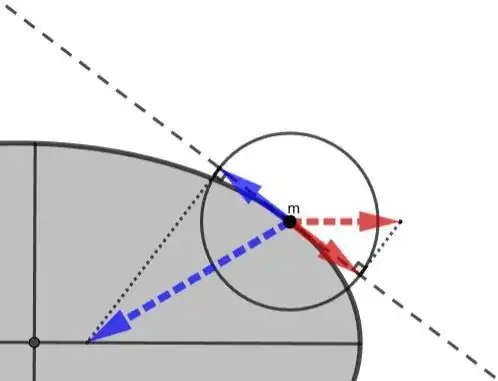
Due to the slope, the buoyancy force is not exactly opposite in direction to the force of gravity. That not-exactly opposite gives a resultant force, which provides the required centripetal force.
The following diagram goes towards explaining why the rotating parabolic dish model is analogous to the rotating Earth.
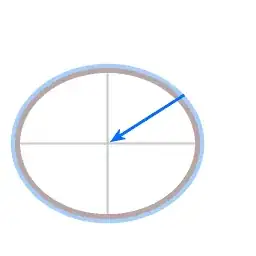
Forces on a rotating celestial body
The Earth has an equatorial bulge due to its rotation.
In the diagram, the equatorial bulge is very much exaggerated for the purpose of demonstration.
(In the case of the actual Earth, the polar radius is $6357 \ \text{km}$, and the equatorial radius is $6378 \ \text{km}$. The difference is about $21 \ \text{km}$.)
Blue arrow: gravity
Red arrow: buoyancy force
Green arrow: resultant force of gravity and buoyancy force.
The following animation presents a case of motion over the surface of the parabolic dish, simplified to the barest essentials.
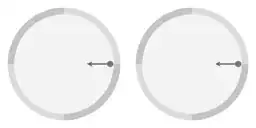
Motion over the surface of a parabolic dish
For a more vivid display, the speed is exaggerated.
The arrow represents centripetal force, arising from the slope of the surface.
The animation represents the case that the object, represented as a black dot, has a velocity relative to the rotating system. There is an oscillation of radial distance and an oscillation of angular velocity. The centripetal force is in linear proportion to the radial distance, which means it is a force according to Hooke's law. When the force that is acting is according to Hooke's law, the resulting motion is harmonic oscillation.
In the animation, the display on the left-hand side represents motion relative to the inertial coordinate system. The display on the right-hand side represents the motion as seen from a co-rotating point of view.
The following parametric equation describes the motion:
$$ x = a \cos(\Omega t) \quad \text{and} \quad y = b \sin(\Omega t),$$
where
$a$ is half the length of the major axis
$b$ is half the length of the minor axis
$\Omega$ is $360^\circ$ divided by the duration of one revolution.
The dynamics
With all of the above in place, we can consider the dynamics of the motion as represented in the motion-over-the-surface animation.
I will divide the description into 4 stages:
- At the point of largest radial distance, the object is circumnavigating slower than the rotation rate of the system. So, at that stage, there is a surplus of centripetal force, and subsequently, the object is pulled closer to the axis of rotation.
- As the object is pulled closer to the axis of rotation, it picks up speed because the centripetal force is doing work.
- At the point of the smallest radial distance, the object is circumnavigating faster than the rotation rate of the system. At that speed, there is not enough centripetal force to keep the object at that radial distance, and due to the object's momentum, it will overshoot, and the radial distance will increase again.
- As the radial distance increases again, the object loses velocity because the centripetal force is slowing it down.
All of the considerations above transfer to the case of motion of buoyant mass over the surface of the Earth.
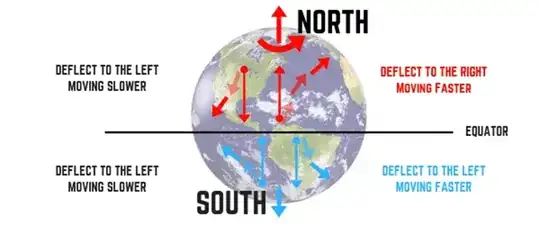
When air mass is flowing in west-to-east direction, then that air mass is circumnavigating the Earth's axis at a slightly faster rate than the Earth itself is rotating. We have that the centripetal force arising from the slope of the Earth's surface is precisely the amount required for co-rotating motion. The air mass flowing in west-to-east direction will swing wide, so it will tend to deviate from the latitude line it is flowing along towards the Equator.
Conversely, when the air mass is flowing in east-to-west direction, it is circumnavigating the Earth's axis at a slightly slower rate than the Earth itself is rotating. Now, there is a surplus of centripetal force, and that surplus will pull the moving air mass to the inside of the latitude circle that the air mass is flowing along.
(Another way to visualize the cases of west-to-east and east-to-west motion: think of a road circuit with steeply banked corners (Example: the banked corner of the test track operated by the tyre manufacturer Continental; the Contidrome.) Let a car be going along a steeply banked corner. If the car is going too slow for the incline of the banked corner, then the car will tend to slump down the incline. Too fast: the car will tend to drift wide.)
The following is crucial:
In the case of the parabolic dish model and the actual Earth, the required centripetal force is provided by the resultant of gravity and buoyancy force. Here, I am using the expression 'buoyancy force' in the widest possible meaning. Layers of air mass are carried by layers of air mass beneath it. Ultimately, weight is carried by the Earth.
By contrast, when you throw an object such that it proceeds in ballistic motion then there is no buoyancy force; the motion is affected by gravity only (with optional consideration of friction effect).
This distinction is essential: the motion of a buoyant object will not be the same as that of a ballistic object because the buoyant object is subject to both gravity and buoyancy force, whereas the motion of a ballistic is affected by gravity only.
This means that it's not a good idea to try and use visualizations of ballistic motion to help you understand the motion of air mass over the surface of the Earth. Those are different cases: depending on the specific circumstances, the motion can come out sort of the same or in the opposite direction; you can definitely not rely on it.
Acceleration relative to the rotating system
In this section, I will derive an expression for the magnitude of the acceleration relative to the rotating system for an object that is subject to a centripetal force, with the force profile as a function of distance according to Hooke's law.
Repeating the parametric equation that describes the motion relative to the inertial coordinate system:
$$x = a \cos(\Omega t) \quad \text{and} \quad y = b \sin(\Omega t).$$
The parametric equation can be rearranged as follows:
$$ x = \frac{a+b}{2} \cos(\Omega t) + \frac{a-b}{2} \cos(\Omega t) $$
$$ y = \frac{a+b}{2} \sin(\Omega t) - \frac{a-b}{2} \sin(\Omega t).$$
After transformation of the motion to the rotating coordinate system, the motion relative to the co-rotating coordinate system is as follows:
$$\begin{align}
x &= \frac{a-b}{2} \cos(2 \Omega t) \\
y &= - \frac{a-b}{2} \sin(2 \Omega t).
\end{align}$$
Notice that the motion along the small circle (the motion relative to the co-rotating coordinate system) cycles with a frequency of $2\Omega$.
I will refer to the motion depicted on the right-hand side of the animated GIF as 'motion along the epi-circle'.
The next step is to obtain an expression for the acceleration of the moving object relative to the co-rotating coordinate system.
Let $a_c$ be the acceleration relative to the co-rotating coordinate system.
We take advantage of the fact that the motion along the epi-circle is, in the idealized case, a perfectly circular motion.
In the case of circular motion, the acceleration is perpendicular to the velocity and has this magnitude:
$$ a_c = \omega^2r. \tag{1} \label{eq:1}$$
(I use the lowercase $\omega$ here for the motion along the epi-circle to distinguish it from the uppercase $\Omega$ that I used for the angular velocity of the system.)
As stated earlier, the motion along the epi-circle occurs at twice the frequency of the angular velocity of the system: $\omega = 2\Omega$.
Inserting that into \eqref{eq:1}:
$$ a_c = (2\Omega)^2r \tag{2}\label{eq:2}. $$
Let $v_c$ be the velocity of the object relative to the co-rotating coordinate system. We have the general relation $v=\omega r$. We have, in this case, $\omega=2\Omega$. Combining that gives for this case the expression $ 2\Omega r = v_c$, that we can use to modify \eqref{eq:2}.
After substituting, we obtain the following expression for the acceleration of the object with respect to the co-rotating coordinate system:
$$ a_c = 2\Omega v_c. \tag{3}\label{eq:3} $$
Discussion:
About the three factors in \eqref{eq:3}:
The factor $\Omega$ - the rotation rate of the overall system - is there because of a remarkable symmetry associated with Hooke's law: when the centripetal force is according to Hooke's law, then any circumnavigating motion, circular or ellipse-shaped, has the same period.
The factor $v_c$, velocity relative to the rotating system, is there because the acceleration relative to the rotating coordinate system is proportional to the radius of the corresponding epi-circle.
The factor $2$ also arises from a symmetry of motion, according to Hooke's law, because for every cycle of the overall rotation, the motion relative to the rotating coordinate system goes through its epi-circle cycle twice.
Discussion:
Ballistics
When a projectile is fired, how will it proceed?
As always, first, simplify down to a level where the phenomenon of interest is still there, but factors that do not impact the essence are omitted.
Once a projectile is underway, its motion is subject to gravity only. We can think of the motion of a projectile as orbital motion, except the velocity is way too slow and so close to the Earth that the projectile impacts the Earth's surface in a matter of seconds. However, that doesn't detract from the fact that during that short flight, the dynamics of the motion is the dynamics of orbital motion.
To simplify, we go to the case of orbital motion with constant height above the Earth.
Side remark: for orbital motion, the oblate shape of the Earth has some effect, but for the purpose of this discussion, that particular effect is negligibly small, so I omit discussion of that.
Orbital motion around a celestial body has the following property: the plane of the orbit goes through the centre of gravitational attraction. That means the plane of the orbit is such that the centre of gravitational attraction is in the plane of the orbit. It follows: the intersection of the plane of the orbit and the surface of the Earth is a great circle.
The ground track of an orbiting object follows the point on the surface that is straight beneath the orbiting object. ('Straight beneath' is where the line from the satellite to Earth's centre intersects the Earth's surface.)
Now visualize an orbit that is along a plane that is inclined relative to the equatorial plane, for instance, at an angle of $60^\circ$, a pretty high latitude. Now, visualize the ground track of that satellite.
We pick a moment in the orbit where the ground track moves parallel to the local latitude line. Pick the angular velocity of the satellite such that the ground track point moves in west-to-east direction relative to the rotating Earth. A great circle that touches a latitude line bends away from that latitude line towards the Equator.
Now, the more interesting case: again, a moment in the orbit where the ground track point moves parallel to the local latitude line. This time, we pick the angular velocity of the satellite such that the ground track point moves in east-to-west direction relative to the rotating Earth. Then, the ground track point will proceed away from the latitude line towards the Equator.
That is why a bullet that is fired in a direction parallel to the local latitude line ends up deviating from that latitude line.
Incidentally, note the contrast:
An air mass that is moving in west-to-east direction tends to swing wide. Air mass moving in east-to-west direction tends to be pulled to the inside of the latitude line because there is a surplus of centripetal force. But a ballistic object will have a ground track along a great circle, and a great circle bends away from a latitude line that it touches either way, both in west-to-east direction and in east-to-west direction.
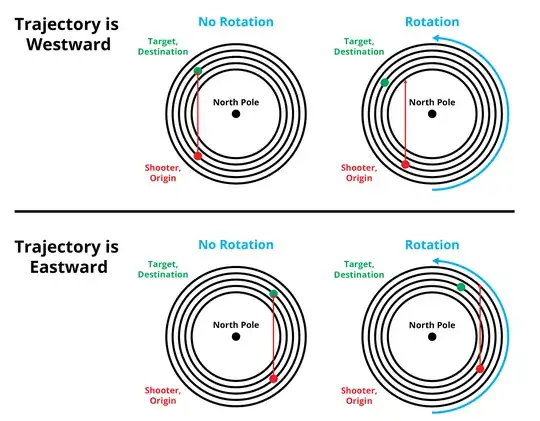Each circle is a different latitude. In a non-rotating context, the arc path of the bullet passes through higher latitudes before falling back to the original latitude. The rotation then adds an additional eastward force vector to the bullet. When firing Westward, that Eastward force vector makes the bullet stop early from returning to its original latitude. When firing Eastward, the additional Eastward vector from rotation makes the projectile overshoot its initial target and continue-on to a lower latitude.
