Tyson claims our weight is the same at the North Pole as it is at the equator: Link. That the equatorial bulge lying outside a spherical shape doesn't exert gravity.
I'm pretty sure this is wrong but I thought I'd ask the opinion of people who know more physics than I.
The geoid is a surface of constant geopotential which is the sum of Earth's gravitational potential and the centrifugal potential arising from the Earth's rotation. In other words, it is the surface on which objects experience no net tangential acceleration.
The effective gravitational field strength, commonly denoted by $g$, is the negative gradient of the geopotential. A function being constant on a surface does not imply that the magnitude of its gradient is also constant. There is around a 0.7% variation in $g$ from the equator to the poles.
In addition, it is obviously not true that "the equatorial bulge lying outside a spherical shape doesn't exert gravity". The bulge exerts gravity like all mass does. If the mass of the bulge itself is neglected when calculating the size of the bulge, the result obtained will only be half of the actual value, as explained in this post.
Neil DeGrasse Tyson is simply wrong.
The simple fact is you weigh more at the poles than at the equator even when you don't take centrifugal force into account. Tyson makes it clear he is talking about the combined effect of gravity and centrifugal force (so this is what would actually be measured if you stood on some bathroom scales). Things only get worse for Tyson, when centrifugal force is taken into account as this makes the measured weight at the equator even lower than at the poles.
The purely gravitational acceleration at the poles ($g_P$) and the equator ($g_E$) is:
$$g_P = C_P\times \frac{GM}{a^2} \approx 1.002639640 \times \frac{GM}{a^2} \approx 9.82462 \ \mathrm{m/s^2}$$
$$g_E = C_E\times \frac{GM}{a^2} \approx 1.000197992 \times \frac{GM}{a^2} \approx 9.81815 \ \mathrm{m/s^2},$$
where $C_P$ and $C_E$ are constants for measurements orthogonal and parallel to the equatorial plane and $a$ is the equatorial radius. The constants depend on the eccentricity and is given by $e = \sqrt{1-b^2/a^2} = 0.08108202$, where $b$ is the polar radius. See the excellent answer by @Ghoster to a related question for where the equations and constants come from.
There is not much difference in the purely gravitational contributions, but this is because the Earth is not very oblate and the difference increases with increased eccentricity.
The centrifugal acceleration at the equator is:
$$g_C = \frac{v^2}{a} = \frac{465.1^2}{6378000} = 0.03391627 \ \mathrm{m/s^2}$$
When the centrifugal acceleration is subtracted from the purely gravitational acceleration, the overall acceleration at the equator is:
$$g_t \approx 9.81815 - 0.033916 \approx 9.78423 \ \mathrm{m/s^2}.$$
These results are in excellent agreement with published measurements.
P.S. What is equal everywhere on the surface of the Earth at sea level is the rate that clocks run at. The time dilation factor is a function of gravitational potential (gravitational time dilation $ \sqrt{1+2\Phi/c^2}$) and the tangential velocity (kinetic time dilation $\sqrt{1-v^2/c^2}$). The higher gravitational potential at the equator means the gravitational time dilation at the equator is slightly less than at the poles, but the increased kinetic time dilation at the equator due to the tangential velocity at the equator exactly compensates. [As mentioned in another answer]2, the combined gravitational potential and centrifugal potential is also the same everywhere on Earth, at sea level.
Tyson is fine. Two things cause the earth's sea level to not be a sphere. Self gravitation of a rotating fluid surface is one of them. It works as Tyson stated and does not cause the gravitational anomalies you mentioned. The other is the moon (and lesser ephemera). The moon's mostly equatorial orbit exacerbates the eccentricity somewhat more than self gravitation can account for. That's where your differences come from. And yes, you would become weightless at the poles if you became weightless at the equator if that was stable under self gravitation, but it isn't for fluids. – Phil Sweet
The disturbance due the Moon causes the bulge to vary twice a day and we call this variation the 'tide'. Generally when talking about gravity at sea level, we are talking about the average sea level. The graph below is the force at the equator (green) and the force at the poles (red) both as a function of eccentricity as the Earth spins faster and flattens out.
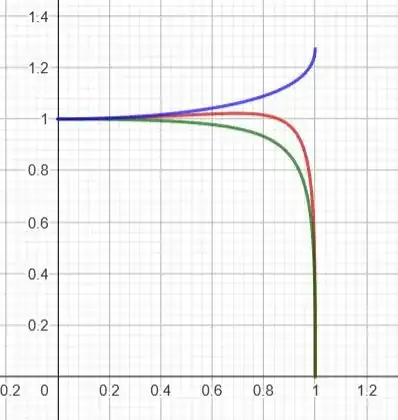
The blue curve is the ratio of the force at the poles to the force at the equator and it can be seen that the polar force is always greater than the equatorial force for any eccentricity, except for $e=1$, where the ratio is undefined. For the force to be zero at both the equator and at the poles (as Tyson claims), the eccentricity would have to be unity and that would mean the elliptical shape of the Earth has flattened out to an infinite radius with zero height, which is not physically possible. To be clear, Tyson is talking about a non rigid Earth that flattens out as it spins, but it should be clear that the force at the poles never goes to zero, except when the thickness of the Earth goes to zero, which is not possible.
The gravitational potential is the same everywhere on "The" geoid. The definition of it is an equipotential surface.
That it has undulation (on the order of a few hundred meters) means the $\vec g$ is not constant. When the local field is stronger, the geoid goes up (and vice versa), with the effect that the ocean rises over sea mounts and dips into the trenches---weird..it seems backwards if you thing in terms of force, but not if you think in terms of energy.
The geoid itself is a correction to "the" ellipsoid--which already has the quadrupole flattening term in it. Perhaps NdGT was referring to gravity on an ellipsoid (for a uniform smooth ellipsoidal planet), and no, it's stronger at the poles. In the extreme limit that earth were to spin just under the time of a LEO orbit (say 120 minutes)...objects at the equator would almost be in orbit, and would experience very little gravity.
Note: the "the" was air-quotes because there is on "the geoid" for reasons:(https://www.ngs.noaa.gov/PUBS_LIB/EGM96_GEOID_PAPER/egm96_geoid_paper.html) and while the ellipsoid is much simpler: it's just a shape on which to define (authalic) latitude, longitude, and height--there are still a whole bunch of them...some global, some local.
