This paper by Arosh et. al. discusses the emergence of limit cycles in the quantum phase space (the Wigner function) for nonlinear oscillators.
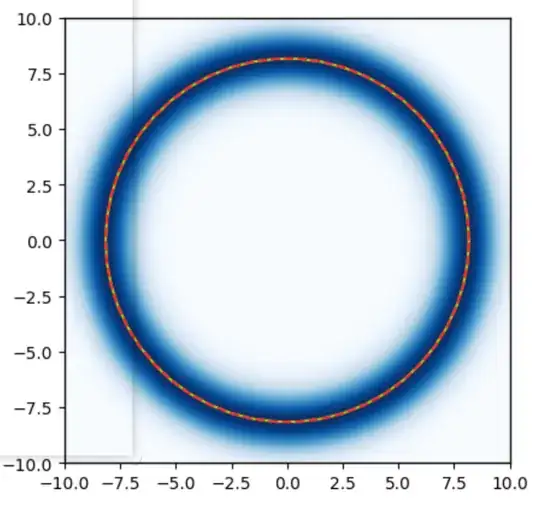
(The quantum limit cycle of the quantum RvdP oscillator in the semiclassical limit, depicted with the nonnegative Wigner function. The yellow solid line shows the classical limit cycle. The red dashed line shows the Wigner function maximum. I made this with QuTiP.)
Here is an interesting property. In the semiclassical limit—where the quantum equations (approximately) reproduce the classical equation—the classical limit cycle coincides with the Wigner function maximum.
My first thought is that, "Well, this is nothing strange. The classical limit cycle coincides with the most probable part of the Wigner function. So, the quantum limit cycle is just the classical limit cycle getting spread out by quantum noise (i.e. the Heisenberg uncertainty principle)."
However, after reading through the phase space formalism literature, I conclude that my initial thought is nonsensical since the Wigner function can not be a true probability distribution due to the uncertainty principle. The Wigner function maximum may not be interpreted as the most probable part of the quantum limit cycle.
I have also read questions on this site regarding Wigner functions (such as this one), and concluded that the Wigner function by itself means nothing more than the phase space representation of the density matrix. There is no telling about physical quantities without taking phase space integrals or some Moyal products. I have tried taking the marginal of the Wigner function by integrating over $p$ to get the $x$ probability distribution, but nothing interesting can be found there. The most probable position has no clear relation to the classical limit cycle radius and is (unsurprisingly) peaked near the origin for the quantum limit cycle I present above.
In any case, the coincidence between the classical limit cycle and the peak of the Wigner function intrigues me, and I am curious about how the community interprets this.