2

I have read the following answer and wish to know whether this is true because I thought the normal force will always pass through the centre of mass of the ball?

"A rolling ball slows down because the normal force does not pass exactly through the CM of the ball, but passes in front of the CM."

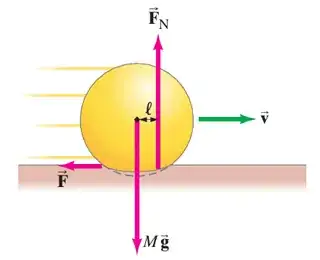
enter image description here

Qmechanic
  • 220,844
Dubious
  • 179

5 Answers5

3

The ball slows down due to rolling resistance. That resistance equals the normal force times the coefficient of rolling resistance.

Rolling resistance occurs due to inelastic deformation of the ball material. The effect of that deformation is to dissipate heat from internal friction and cause an asymmetric distribution of the normal pressure, thus shifting the location of the normal force.

Hope this helps.

Bob D
  • 81,786
2

When a ball or other object is sitting still, the normal force does pass through the center of mass. You can see this must be so from your diagram. If it did not, there would be a torque and the ball would rotate.

Stand up. The normal force originates from each point on the bottom of your feet. Each of those forces creates a torque. Since you are standing still, the total torque is $0$.

You stand up by pushing the floor away with your legs. Push a little less with one leg. You immediately begin to rotate.

For more, see Toppling of a cylinder on a block and Why do we assume weight acts through the center of mass?

mmesser314
  • 49,702
1

See in the figure center of mass has nothing to do with it, since this ball will slow down due to the rotational resistance and frictional forces applying on it (F) (I feel sorry for not putting a vector sign).

the center of mass doesn't play any role in decelerating the ball but they are the microscopic interaction and energy loss due to deformation which creates a gradual deceleration. The center of mass's role is more about the distribution of mass in the ball, which affects how it rolls but not why it slows down.

Thank you

Shivansh Maheshwari
  • 314
1

If the ball rolls without slipping while slowing down, there must be:

  • a net torque acting to reduce its rotation rate ($\tau = I \frac{d \omega}{d t}$) and
  • a net force acting to reduce its velocity ($F = m \frac{d v}{d t} = mr \frac{d \omega}{d t}$).

Here torque is $\tau$, moment of inertia is $I$, angular speed is $\omega$, mass is $m$, and speed is $v$. The contact forces (friction and normal force) produce the net torque about the centre of mass of the ball. Thus their sum cannot act through that centre of mass.

It would be possible for a perfectly rigid ball to slow down via rolling friction, even though the normal force acts through the centre of mass, if slipping were allowed. However, the case in the illustration you provide relies on the deformation of the ball. Therefore the normal to the point of contact does not pass through the centre of mass and a net torque results.

FTT
  • 1,874
  • 5
  • 9
0

Well, because of the force between the ball, and the surface it is rolling on, the ball, and the surface deforms a small amount, and as it is rolling, both deformations must propagate forward with the ball. Therefore, the force, and the size of the deformation in front of the ball must be slightly larger than they are behind the ball. This causes the aggregate sum of the forces between the ball and the surface to be slightly forward of the point directly underneath the center of mass.

Charles Bretana
  • 190