So to make this work, you need to follow a standard form for SR problems.
Name everyone in alphabetical order: Alice, Bob, Charlie..., in frames $S$, $S'$, $S''$, ...
Introduce the "at rest" frame 1st, and so on.
Talk about events $E = [t=0, x=0] = [t'=0, x'=0]'$ I've decided to use square brackets for events, so they 'pop' visually.
Start at the origin: $[0, 0]$.
Really, there is no reason to start at $t=5$, it's one more detail to cause confusion.
So: Alice fires a photon at:
$$ E_0 = [0, 0] $$
Bob (formerly Joe) at this time, in $S$ is at:
$$ E_1 = [0, 4] $$
an closing at $\gamma=2$ (or $\beta=\frac 1 2 \sqrt 3$, or $\omega={\rm arctanh}(\beta)$...it doesn't matter how you specify it).
....OK, now we see the problem. When doing relativity of dealing with Minkowski diagrams, and Zo is correct: draw a Minkowski diagram, the origins of Alice (you) and Bob (Joe) need to overlap.
So now I need to work backwards, in my head. Thanks.
We need to move the origin up by $4/({\sqrt 3}/2)= 8/\sqrt{3}$, which is the event when Alice and Bob are co-located in spacetime.
I quit. Rephrase the question in the frames I have described and the answer will be clear. (Note, if you can't put the problem in this form, it's ill-posed, or it's too complicated to be pedagogical).
Edit: OK, I'm trying again. The definitive answer to:
Is the problem just that we couldn’t start our clocks at the same time?
is "YES". The way the problem is set up, the absolute clock bias is meaningless. Joe and you, as the problem is posed, do not share a common origin event $O$:
$$ O \equiv [t=0, x=0] \equiv [t'=0, x'=0]' $$
which precludes the use Lorentz transformations.
Since Joe is approaching you, there is an event that is the crossing of your world lines--this should be the origin of $S$ and $S'$.
The nuisance that led to putting it on hiatus was your choice of $\beta=\sqrt(3)/2\approx 0.866....$ it's (mathematically) irrational, and is not nice for a good Minkowski diagram.
If you pump the brakes a bit, and set $\beta=\frac 4 5=0.8$, then Pythagorus kicks in and:
$$ \gamma = \frac 1 {\sqrt(1-\frac{16}{25})} = \frac 5 3 $$
So I'm just going to go with those.
Now I can define coordinates, which you can draw on a Minkowski diagram (exactly if you have 15 sub-tics per integer tic-mark):
You are in $S$, and your world line is:
$$ W_A(t) = [t, 0] $$
and Joe (aka Bob) is on:
$$ W_B(t) = [t, \beta t] $$
This is nice, we have both your worldlines well defined in your coordinates, as a continuous set of events parameterized by your clock.
The question specifies that you fire a photon when $x_B=-4$, which we can now read off Joe's worldline:
$$W_B(t, x)_x = \beta t = -4$$,
so we call that event $E_1$ and see that occurs at
$t_1 = x_1/\beta = -4/(4/5) = -5$, making your coordinates
of the event:
$$E_1 = [-5, 0] $$
That is you firing a photon in your frame. We can now find where Joe is when that happens (using your definition of simultaneity, which is equal time-coordinates $\forall x$):
At this time, Joe's world line puts him at:
$$E_2 = W_B(t_1, \beta t_1) = [-5, -4] \equiv [t_2, x_2] $$
(note: integers, nice).
So what does Joe see? Since we have events in co-origin'd frames, we can use the Lorentz Transform:
$$t'_2 = \gamma(t_2-\beta x_2) = \frac 5 3(-5 - \frac 4 5 (-4)) = -3
$$
$$ x'_2 = \gamma(x_2 - \beta t_2) =
\frac 5 3(-4 - \frac 4 5 (-5)) = 0
$$
(where the zero is required, since Joe is always at $x'=0$).
Thus:
$$E_2 \equiv [t'_2, x'_2]' = [-3, 0]'$$
where the prime, $)'$, means the coordinates are in $S'$ (I prefer this over saying $E'_2$ because events are points in Minkowski space, and they are the same thing in all frames, they just have different coordinates in different frames. Maybe $\{t, x\}_S$ and $\{t', x'\}_{S'}$ are better--we're trying to maximum clarity--but there is only so much MathJax that I can do).
Meanwhile, we can LT your photon emission into Joe's coordinates:
$$t'_1 = \gamma(t_1-\beta x_1) = \frac 5 3(-5 - \frac 4 5 (-0)) = -\frac{25} 3
$$
$$ x'_1 = \gamma(x_1 - \beta t_1) =
\frac 5 3(0 - \frac 4 5 (-4)) = +\frac{16}3
$$
and he puts your transmission at
$$ E_1 = [-8 \frac 1 3, +6 \frac 2 3]' $$
Now I hope you see the problem. You simply cannot agree on a synchronous time to emit your photons.
We can define a third event: Joe's position when he sees you transmitting, which is defined by his definition of simultaneity:
$$ t'_3 = t'_2 = -\frac{25} 3 $$
and of course (which is why we colocated the origins of $S$ and $S'$):
$$ x'_3 = 0 $$
so that:
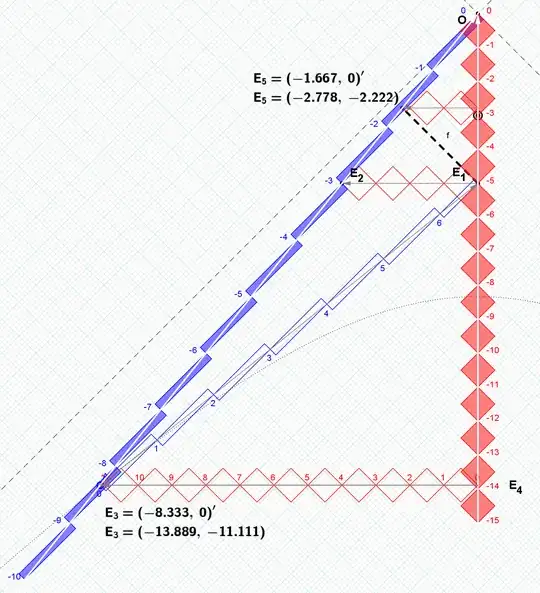
$$ E_3 = [-\frac{25} 3, 0]' $$
which we can inverse LT back to you:
$$ E_3 = [-\frac{125} 9, \frac{100} 9] $$
which defines a 4th event:
$$ E_4 = [-\frac{125} 9, 0] $$
which is YOU when you see that JOE sees YOUR transmission. That is, $80/9$ seconds before you transmit, Joe is seeing you transmit, and when you actually transmit, Joe says you transmitted:
$$ t'_2-t'_3 = 2\,{\rm seconds} $$
ago. (Note: this is why using events in well defined frames is critical to understanding relativity. Relying on a sentence like "YOU when you see that JOE sees YOUR transmission" stretches the ability of English verb conjugation...it did not evolve with Special Relativity in mind).
There is still a fifth event: when Joe sees your photon, which occurs at
$$ t_5 = t_1 + \frac{|x_2|}{\beta+c}
= -5 + \frac{4}{9/5} = -\frac{25} 9\,{\rm seconds}
$$
so that Joe's position in $S$ and $S'$ are, respectively:
$$ E_5 = [-\frac{25} 9, -\frac{20} 9] = [\frac 5 3, 0]' $$
Now at this point, I'll let you pick a time for Joe to transmit, and see what everyone sees.
The take aways for the OP on physics are:
Use colocated inertial frames (otherwise, you can't LT)
Talk about Events (otherwise, it is far to confusing)
Pick nice $\beta$, $\gamma$, if possible (seriously, you can see why I bailed at $\sqrt(3)$. Pythagorean triples are a good start).
Take Away for OP on PSE:
- Read the comments on your post and respond. They are their to help.
Take aways for downvoters:
- Don't down vote the only attempt to actually answer the question. New serious students will ask mixed up questions, especially in SR and quantum mechanics (source: https://physics.stackexchange.com), and such questions may not admit a proper answer, so any answer is by definition -1. You can downvote the question, but that is not very inviting to noobs, we don't want this site to go the stack overflow route of gate-keeping code nerds. We're here to help noobs. j/s.