Quadrupole potential generation in Paul traps

Question

I am currently getting familiar with the concept of the Paul trap and the underlying physical principles. I do understand what kind of potentials are needed to trap charged particles, e.g. for the 3D paul trap or the quadrupole mass filter. However, I am struggling with how these potentials are created by different geometries and the applied voltages.

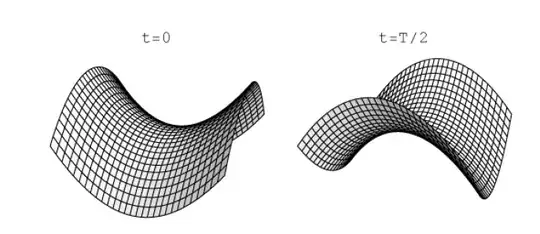
Why is it that applying voltages $$U=U_{DC}+U_{AC}cos(\omega t)$$ and $$U=-(U_{DC}+U_{AC}cos(\omega t))$$ to this kind of electrodes creates a potential of the form $$V=k\cdot (U_{DC}+U_{AC}cos(\omega t)) \cdot (x^2+y^2-2z^2) \text{ ?}$$ I do see that the shape of the ring electrode kind of resembles a positive and the shape of the endcap electrodes resembles a negative equipotential surface in this very potential.

Does that mean that whenever one is looking for a geometry yielding a certain electric potential, one can just take electrodes of the shape of the potential's positive and negative equipotential lines/surfaces and apply a positive, respectively negative voltage to them, with the potential in all other regions of space following automatically? If not, why is it that this works in the given case?

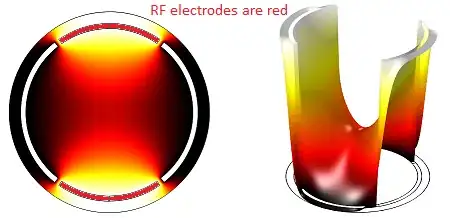
However, there is also the often used geometry of four cylindrical electrodes that creates a two dimensional trapping potential along the cylindrical axis. Following the notion from before (and neglecting the small deviations between the hyperbolic and the cylindrical shape), one would simply apply voltages $U$ and $-U$ to two pairs of opposing electrodes and get a potential of the form $$V=k\cdot U \cdot (x^2-y^2)$$ (since with the z-axis being parallel to the cylindrical axis, the shape of the electrodes more or less resembles positive and negative equipotential lines in the y(x)-diagram). However, while some sources state that this can be done, I also found very reliable sources like this publication stating that one can also simply apply an AC voltage to one pair of electrodes and connect the others to ground.

Wouldn't that mean that you don't even have a quadrupole anymore? Why is it that this still works and creates the kind of potential that is needed?

I'd be very thankful for any hints or answers helping me to understand the matter.

Best regards

Answer 1

Radio frequency Paul traps confine charged particles without applying any magnetic fields (As in Penning traps), but since confining charged particles only using electrostatic forces is impossible according the the Earnshaw's theorem, a quasi-static approach is taken, and the particles are trapped dynamically.

Radio frequency ion traps do this by forming a potential with a saddle point (which confines the particle in all but one direction), and then changing the unstable direction by applying a sinusoidal potential to the the electrodes:

In the above figure the particle is first confined in the left-right direction, and in the second half of the period becomes confined in the perpendicular direction.So, the particle is always confined in one direction and unstable in the other direction, and theses stable and unstable directions are interchanging constantly with a high enough frequency to prevent the particle from escaping.

So, the only critical feature of a confining potential is having a saddle point. There is no restriction on the shape of the electrodes as long as they form a potential with a saddle point. Many RF traps with different electrode shapes are proposed based on this principle. For example, cylindrical Paul traps, spherical Paul traps, linear four-rode Paul traps (what you mentioned) and various surface electrode Paul traps all have a shape other than the hyperbolic shape of a conventional 3D Paul trap.

A surface electrode trap (left) and the potential above it (right):

Cross section of a spherical trap (left) and the height expression of the potential inside (right):

In both cases you see that a saddle point in the potential exists.

The main difference between these traps and the hyperbolic Paul trap is that although in all cases a saddle point exists at the point (or line) of confinement, but only for the ideal hyperbolic Paul trap the potential is quadrupolar. For other geometries, higher order multipole terms appear in the potential, that may have desirable or undesirable effects based on the application. The quadrupole potential leads to the standard (linear) Mathieu equation for the motion of the trapped particles, but the higher order fields add nonlinearities to this equation. For example, in mass spectrometry these nonlinearities may cause the particle to pick energy from the field and eject form the trap unexpectedly (resonant ejection). Nonlinear traps are analyzed in some papers, e.g. this one.

In conclusion, it is not necessary to have hyperbolic shaped electrodes, and those electrodes can be replaced by arbitrary-shaped electrodes like two spheres and a circular ring so long as they are arranged in the same as before _ that forms a saddle point in the potential _. This is way the linear Paul trap and many other non-hyperbolic traps works. The only advantage of having hyperbolic electrodes is linearity of the equations of motion.