1st question:
Qualitatively, the reason the ions drift to the center is that the center of the trap is a point of dynamic stability for the ions, and ions experience a pondermotive force toward the center. I have explained this more in my answer to this question. The particle is always unstable in one direction but since that direction changes with the RF drive frequency, the particle is dynamically trapped.
The following is a typical trajectory of the ion in such a trap, which shows the closed path of the particle as well as small oscillations at the frequency of the RF field.

2nd and 3rd questions:
If the potential inside the Paul RF trap is exactly quadropolar (which is the case for hyperboloid electrodes), then the equations of motion will be in the form of Mathieu equations. These equations have two parameters $(a,q)$ which depend on the physical paramters of the problem:
$$a_z = -\frac {8eU} {m r_0^2 \Omega^2} \qquad\qquad q_z = \frac {4eV} {m r_0^2 \Omega^2} $$
for the x direction equation (as stated in the Wikipedia article.). They depend on the RF voltage V, DC voltage U, RF frequency $\Omega$ and the particle's charge to mass ratio.
Now, there are a couple of region of stabilities for the $(a,q)$ parameters in $(a,q)$ plane which are the allowed (a,q) parameters that lead to a stable motion of the ion in the trap. Therefore, the frequency $\Omega$ alone cannot lead to (in)stability of the motion. The lowest order (and largest) of these regions is this:
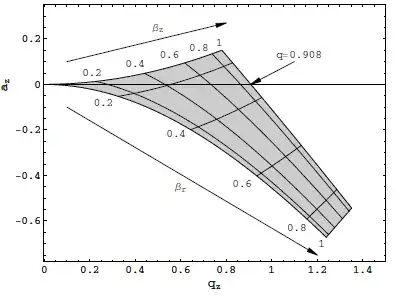
As you can see now, for a given frequency and voltage there are many possible charge to mass ratios that can be trapped. Note that practically you cannot increase $V$ or $\Omega$ too much as this can lead to other effects such as radiation or even electrical breakdown in the trap. The above plot is the 1st stability region. There are other stability regions too but they're rarely used because of the practical difficulties.
If you want to trap more than one particle in the trap simultaneously, you may need to consider Coulomb interactions among the particles which can cause their motion to become unstable. but other than that, it is possible to do that, and is actually done in practice because it's difficult to only insert one single particle into the trap.

