Does A Pivot Exert A Force

Question

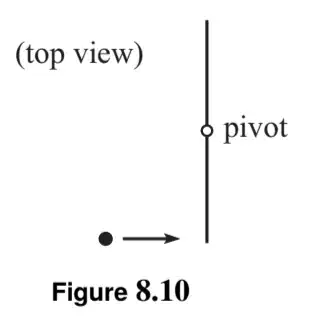
On a frictionless horizontal table, a uniform stick is pivoted at its middle, and a ball collides elastically with one end, as shown in Fig. 8.10. During the collision, what are all the quantities that are conserved in the stick-plus-ball system?

(a) L around the pivot
(b) L around the pivot, E
(c) L around the pivot, p, E
(d) L around the point of collision, E
(e) L around the point of collision, p, E

Now, when I solved this, I got answer choice $B$, which was right for what seems to be the wrong reasons. Once the stick is collided with, I thought there would be a centripetal force, meaning $p$ is not conserved. However, the component of the centripetal force orthogonal to the stick is $0$, so I thought there is no net torque around the pivot leading me to assume $L$ around the pivot is conserved. Finally, because the table is frictionless, I assumed mechanical energy is conserved.

There are probably a couple things wrong with my solution, because it fails to explain why $L$ around the point of collision is not conserved. Furthermore, the official solution seems to imply that the pivot of the stick exerts some kind of force orthogonal to the stick.

The solution:

$\boxed{b}$ There is an external force at the pivot on the stick-plus-ball system, so p isn’t conserved (the earth will gain momentum). But this force doesn’t ruin conservation of L around the pivot, because the lever arm of the force is zero, so there is no torque. E is conserved by definition, since we’re assuming the collision is elastic. Furthermore, choice (d) isn’t correct, because the force from the pivot does provide a torque around the point of collision, since the lever arm is now nonzero.

I was confused about the force at the pivot (normal to the stick) that the solution refers to. By definition, the stick is pivoted around the center, so the velocity of the center of the mass of the pivot is $0$. Does this imply that the pivot has an extremely large angular velocity to account for whatever force the pivot exerts (to keep it in place)?

I'm not quite sure where this force is coming from either, because the problem doesn't tell us whether the ball accelerates or not, so if we assume the ball to have a constant velocity, it doesn't exert any kind of force whatsoever.

Could someone explain why my solution is wrong, as well as what force the pivot exerts that the solution is referring to?

Answer 1

Before the collision, the ball moves to the right, as per the arrow. Assume it has speed v0.

After the collision, the ball could have various different velocities but if the stick has inertia, they must be less than v0 (in magnitude) and along the same arrow direction (positive or negative). The details would be determined by the length and inertia of the stick, which we are not given.

This requires an impulsive force ON the ball at the end of the stick that is parallel to the arrow and opposite in sign.

Which means there is a force ON the stick in the direction of the arrow.
Since the center does not move, we know that the net force on the pivot and stick is zero.

Which means there is a force ON the pivot FROM the ground in the opposite direction as the arrow.

Answer 2

Imagine the rod has no pivot and the rod is free to translate or rotate naturally of the perfectly frictionless surface. Lets say after the collision the end of the rod where the impact occurred moves away at velocity v. The last point of the rod to start moving is the part furthest from the impact. This means the centre of rod is moving at a velocity of v/2. When a pivot is present (i.e. there is literally a hole drilled in the table top and shaft for the rod to pivot around), the centre of the rod is prevented from moving st v/2 and there must be a force acting in the opposite direction that cancels out the force that would have caused the centre to accelerate to v/2.

Answer 3

Answers from the comments

From @mmesser314

A pivot does exert a force. You can see this by hanging a pendulum from one. The pendulum does not fall down. If you hold the bob off to the side, gravity exerts a torque and accelerates the pendulum, and then decelerates it on the other side. The pivot holds the pivot point fixed. It is a reaction force just like the force that keeps a mass from sinking into a table top. The force is exactly strong enough to hold the point fixed.

This might help you think about torque: Toppling of a cylinder on a block

From @Solomon Slow

Your diagram is missing something: A pivot is a kind of bearing—a mechanical connection between two parts of a machine that allows some restricted type/amount of relative motion between the two parts, while preventing other motions. It only makes sense to say that the stick rotates on a pivot if the pivot is connected to something else. It allows the stick to rotate with respect to some support structure, while preventing translational motion between the stick and the support. And, it prevents translation by transmitting force.