Physical meaning of symmetric and antisymmetric wavefunction

Question

On describing Bosons and Fermions, the symmetry of wavefunction is introduced first. Here, If two particles a and b, are in two states n and k respectively, we get the wavefunction individually. On changing the position of particles between two states earns another wavefunction. But ,the overall general wavefunction is written in two linear combinations (this complicated description is simplifed in the picture below). Why if particles are interchanged, we get symmetric and anti symmetric wavefunctions. But what is the physical meaning of sign reversal in anti-symmetric case?

---

Edit: In the picture, the second case should be - particles, a in k state and b in n state.

Answer 1

Firstly, the question refers to the symmetry about particle exchange - the title is confusing, since there are many other important symmetries, starting with $\psi(\pm x)=\pm \psi(x)$, which has to do with the number of nodes in the eigenstates vs. the ground state.

Regarding the particle exchange, the argument given in most quantum mechanics books is that, since the particles are indistinguishable, the physical properties should be independent when we switch any two particles. Wave function is not a measurable quantity itself, but the particle density is. Thus, in a system of two particles we have $$ \rho(x_1,x_2)=|\psi(x_1,x_2)|^2=\rho(x_2,x_1)=|\psi(x_2,x_1)|^2 $$ (Note that a system of particles is generally described by a single wave function.) This means that the wave function under particle exchange may acquire a phase factor: $$ \psi(x_1,x_2)=e^{i\phi}\psi(x_2,x_1). $$ If we exchange the particles twice, we should return to the initial state (this condition is however relaxed in the case of anyons): $$\psi(x_1,x_2)=e^{i\phi}\psi(x_2,x_1)=e^{2i\phi}\psi(x_1,x_2),$$ hence $e^{2i\phi}=1\Rightarrow e^{i\phi}=\pm\sqrt{1}=\pm 1.$

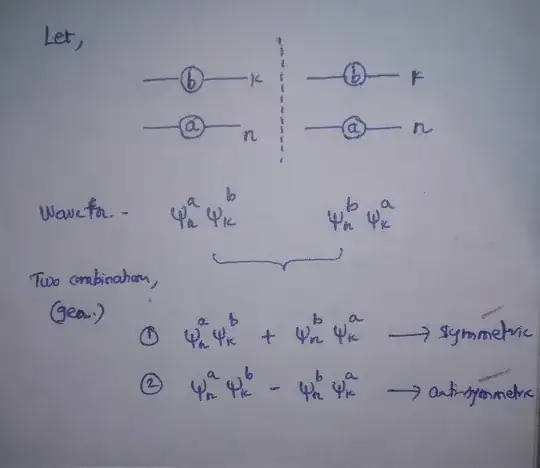
I.e., the wave function is either symmetric or antisymmetric in respect to exchange of any two particles (the discussion above is easily generalized to exchanging any two particles among a larger number of particles.)

In case of non-interacting particles, the eigenstates of the multiparticle system can be represented in terms of one-particle eigenstates, of which one has to form symmetric/antisymmetric combinations to satisfy the condition derived above: $$ \psi(x_1,x_2)=\phi(x_1)\varphi(x_2)\pm \varphi(x_1)\phi(x_2). $$ This is easily generalized to more particles with Slater determinants and permanents.

This innocent game with the phase factor turn out to have far reaching consequences in terms of the particle properties (spin and magnetic moment), their quantum statistics (Bose-Einstein vs. Fermi-Dirac), their interactions, etc.

Related:
Wavefunction of three particles
'Deriving' superposition representations for 3 particles
Why does Hartree-Fock (HF) theory even work?
Why can't you always write the anti-symmetric state as slater determinant?

Answer 2

First of all, states of indistinguishable particles have to be either symmetric or antisymmetric with respect to a permutation $P$ of two particles, which is a parity operation $P^2 = \mathbb{I}$. If a state would not be an eigenstate of $P$, one could use the transformation behaviour to distinguish the two particles.

Now the sign seems like a technicality, but has a vast impact on how many particles interact with each other. Take for instance two fermions in the non-trivial states $\psi_1$ and $\psi_2$, respectively. If two fermions (admitting an antisymmetric wavefunction) would occupy the same state, the two-particle wave function would vanish

$$\psi_1 \otimes \psi_2 - \psi_2 \otimes \psi_1 = 0 \qquad \iff \qquad \psi_1 = \psi_2.$$

Bosons (symmetric wavefunction) on the other hand are allowed to occupy same states, in fact there is a phenomenon called Bose-Einstein condensation that takes this further. So the sign really contains information about allowed states. In the presence of Lorentz symmetry, one can show a relation of the statistics with the spin of the particles. Particles admitting a half-integral spin quantum number can be thought of as a physical interpretation of the sign, see Spin-Statistics Theorem for details.