Resolution of Ehrenfest paradox using only special relativity

Question

It was my understanding the solution to the Ehrenfest paradox requires non-Euclidean geometry. Observers riding the rotating disk measure small distances according to the Langevin-Landau-Lifschitz metric. However this comment claims the paradox is "easily resolvable" with special relativity alone. What is the solution to the paradox using only special relativity?

Answer 1

Instead of a solid disk, we might as well think of a circular train traveling on a circular track.

Alice sits in the station. Bob is riding on the train.

The Question: The track is shorter in Bob's (instantaneous) frame than it is in Alice's. Bob's train car (which is one of many) is longer in Bob's (instantaneous) frame than it is in Alice's. How do we reconcile this?

The Short and Complete Answer: Other train cars (far from Bob's) are shorter in Bob's frame than they are in Alice's, and on average the various train cars are shorter in Bob's frame than in Alice's, by exactly the factor necessary to make them fit on the track.

That is a full answer, but past experience tells me that many people have found it unconvincing, so I am expanding that answer in excruciating detail below. It might be easier to read as a pdf, which I've posted here.

PRELIMINARIES

According to Alice, a rod of length $1$ travels along its own length at speed $v$, while Bob travels in a different direction at the same speed $v$. What length does Bob attribute to the rod?

Answer: We can take the endpoints of the rod (in Alice's frame) to be $(0,0)$ and $(A,B)$, where $A^2+B^2=1$. We can take Bob's direction of travel to be $(0,1)$.

According to Alice, the endpoints of the rod at time $t$ are parameterized as $$\hbox{LEFT: }\quad L(t)=(t,tvA,tvB)$$ $$\hbox{RIGHT: }\quad R(t)=(t,(tv+1)A,(tv+1)B)$$

Translating to Bob's coordinates, we have $$L(t)\mapsto=(0,0,0)$$ $$R\left({vB\over1-v^2B}\right)\mapsto\left(0,{A\over 1-Bv^2},{B\sqrt{1-v^2}\over 1-Bv^2}\right)$$

These are the left and right ends of the rod at a single time according to Bob, so in his frame the length of the rod is the distance between them, which is $${ \sqrt{A^2+B^2(1-v^2)} \over 1-Bv^2}$$ If we take $A=-\sin(\theta)$ and $B=\cos(\theta)$, this becomes $${\sqrt{1-v^2\cos^2(\theta)}\over1-v^2\cos(\theta)}\qquad(1)$$

A CIRCULAR TRAIN TRACK

Alice is stationary with respect to a circular train track of circumference $2\pi$, on which sits a train of the same circumference traveling at speed v in a counterclockwise direction. The track is parameterized by the angle $\theta$. Bob is a passenger on the train, currently at a point that we might as well take to be $\theta=0$.

Consider the point $\theta$ on the track. Alice says that its distance from the center is $\cos(\theta)$ horizontally and $\sin(\theta)$ vertically. The vertical distance Lorentz contracts for Bob to $\sqrt{1-v^2}\sin(\theta)$. Therefore Bob sees the track (at a fixed time $t'$) as the locus of $\big(\cos(\theta),\sqrt{1-v^2}\sin(\theta)\big)$, and its length is $$\int_0^{2\pi} \sqrt{\cos(\theta)^2+(1-v^2)\sin(\theta)^2}d\theta =\int_0^{2\pi} \sqrt{(1-v^2\sin(\theta)^2}d\theta={4 E(v^2)}$$ where $E$ is the complete elliptic integral.

Call this quantity $\hbox{tracklength}(v)$, i.e. $$\hbox{tracklength}(v)={4E(v^2)}\qquad(2)$$

LOCATION OF A SINGLE CAR

At time $0$, let Alice label each point on the train $P_\theta$ where $\theta$ is its current location. The worldline of $P_\theta$, per Alice, is $$\{(t,\cos(\theta+vt),\sin(\theta+vt)\}$$ The same worldline, per Bob, is $$\left\{\left( { t -v \sin(\theta+vt) \over \sqrt{1-v^2} }, \cos(\theta+vt), {\sin(\theta+vt)-vt\over\sqrt{1-v^2}}\right)\right\}$$

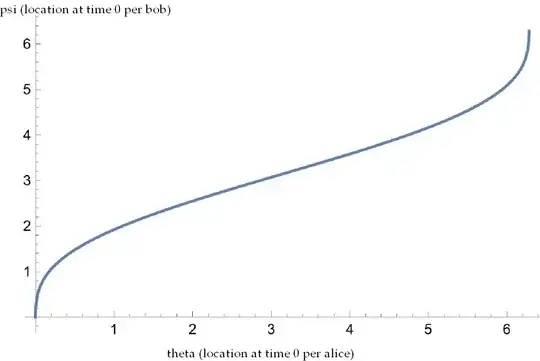
Thus the radial location of $P_\theta$ in Bob's coordinates at time $0$ is $$\psi=\psi(\theta)=\theta+vt \quad\hbox{where $t$ solves}\quad t=v\sin(\theta+vt)$$.

Thus $\psi$ satisfies $$\psi-\theta=v^2\sin(\psi)\qquad(3)$$

$\psi(\theta)$ has the following general shape (illustrated here for $v=.99$):

Note for future reference that if we write primes for derivatives with respect to $\theta$, then (3) implies $$\psi'={1\over 1-v^2\cos(\psi)}\qquad(4)$$

RADIAL EXTENT OF A SINGLE CAR

According to Alice, an (infinitesimal) car labeled $P_\theta$ stretches (at time $0$) from radial location $\theta$ to $\theta+d\theta$. According to Bob, it stretches (at time $0$) from $\psi(\theta)$ to $\psi(\theta+d\theta)$ and therefore covers a radial distance of $$d\psi={d\psi\over d\theta}d\theta= {d\theta\over 1-v^2\cos(\psi)}\qquad(5)$$ courtesy of (4).

Thus if Alice defines a "car" as stretching from $\theta_1$ to $\theta_2$, Bob says that car covers the radial distance $$R(\theta_1,\theta_2)=\psi_2-\psi_1=\int_{\psi_1}^{\psi_2} d\psi=\int_{\theta_1}^{\theta_2} {d\theta\over 1-v^2\cos(\psi)}\qquad(6)$$ (where $\psi_i=\psi(\theta_i))$.

Of course the entire train unambiguously covers a radial distance of $2\pi$, so we must (and do!) have $R(0,2\pi)=2\pi$.

LENGTH OF A SINGLE CAR

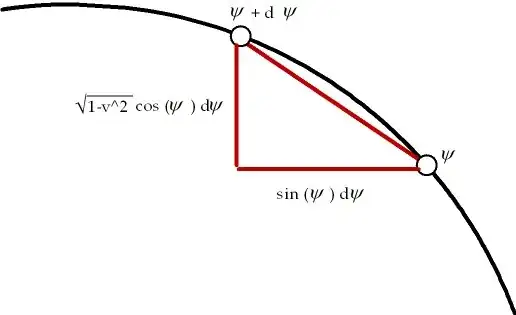
The following picture reflects the track as seen by Bob, with measurements justified by the preliminaries to equation (2):

Thus the linear length of an infinitesimal car at $\psi=\psi(\theta)$ (i.e. the hypotenuse) is given by $$\sqrt{1-v^2\cos^2(\psi)}\quad d\psi = {\sqrt{1-v^2\cos^2(\psi)}\over 1-v^2\cos(\psi)} d\theta\qquad(7)$$ (invoking (5)).

Integrating (7) gives the track length derived in (2): The length of the train must equal the length of the track.

An alternative way to get the length of the car is to treat it as a rigid rod moving along its own length with velocity $v$; then invoke equation (1), which immediately gives the right hand side of (7).

For a non-infinitesimal car, we get the length by integrating (7). Explicitly, for a car stretching from $\theta_1$ to $\theta_2$ per Alice, and from $\psi_1$ to $\psi_2$ per Bob, we have the length $$L(\theta_1,\theta_2)=\int_{\psi_1}^{\psi_2}\sqrt{1-v^2\cos^2(\psi)}\quad d\psi = \int_{\theta_1}^{\theta_2}{\sqrt{1-v^2\cos^2(\psi)}\over 1-v^2\cos(\psi)} d\theta\qquad(8)$$

If we take $\theta_1=0,\theta_2=2\pi$, we get the full length of the train (per Bob), which must (and does) equal the full length of the track (per Bob), given in (2).

EXAMPLE

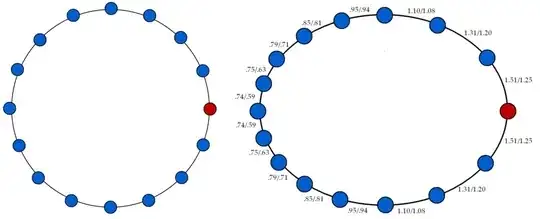
We take the speed of the train to be $v=3/5$.

Alice divides the train into sixteen equal pieces with endpoints as shown on the left. On the right we have the same picture translated into Bob's coordinates (at his time zero). Bob is located at $(1,0)$ (shown in red).

The segments in Bob's pictured are labeled X/Y, where $$X={\hbox{Radial Distance According to Bob}\over\hbox{Radial Distance According to Alice}} \qquad Y={\hbox{Length According to Bob}\over\hbox{Length According to Alice}}$$

The pictures were derived as follows:

1. Alice's track is the unit circle. Bob's track is shortened in the vertical direction by a factor of $\sqrt{1-v^2}=.8$ as in the discussion around equation (2).

2. Alice's dots denote the dividing lines between train cars, with radial coordinates $2\pi k/16$.

3. Alice's radial coordinate $\theta_k=2\pi k/16$ translates to Bob's radial coordinate $\psi_k=\psi(\theta_k)$ where $\psi$ is defined by (3).

4. Each $X$ value is calculated as $$\hbox{Difference between two successive $\psi$ values}\over \hbox{Difference between two successive $\theta$ values}$$ (where the denominator is always $2\pi/16$). (The numerator is as per equation (6).) Because Alice and Bob agree that the full radial extent of the track is $2\pi$, these $X$ values must (and do) average to $1$.

5. Each $Y$ value is calculated as $${L(\psi_{k+1},\psi_k)\over 2 \pi/16}\qquad(9)$$ with $L$ defined in (8).

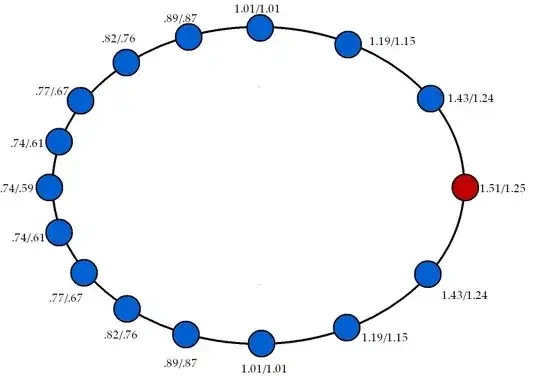
INFINITESIMAL CARS

The example above assumes cars of length $2\pi/16$ (in Alice's reckoning). The blue points in the picture indicate the places where two cars are joined.

For comparison, we can consider a set of infinitesimal cars (of length, say, $d\theta$ according to Alice) located at those same blue points. In the following picture, each X/Y label represents the (radial extent)/length of each car, according to Bob, as a multiple of $d\theta$:

Answer 2

...this comment claims the paradox is "easily resolvable" with special relativity alone.

The comment is correct.

It was my understanding the solution to the Ehrenfest paradox requires non-Euclidean geometry.

The Ehrenfest paradox does not need to be explained by non-Euclidean geometry, but the paradox does provide an insight into why measurements made in a rotating reference frame imply non Euclidean geometry.

Rulers placed on the circumference of a rotating disk are length contracted by the gamma factor $1 / \sqrt{1-v^2/c^2}$, where v is the magnitude of tangential velocity of any point on the rim. This makes the perimeter appear to be longer than $2\pi R$ by the gamma factor. Since this disagrees with the Euclidean expectation, it implies the geometry measured by the accelerating observer in the rotating reference frame is non-Euclidean. Simple as that.

The proper length of the perimeter really is greater than $2 \pi R$. It is not just an artifact of rotating coordinates, If we took a cable with a rest length of $2 \pi R$ and wrapped it around the perimeter and tried to join the ends, the cable would be stretched and would probably break. We can also send light signals in a fibre optic all the way around the perimeter, bounce it off a mirror and send it back to the start and the travel time of the light multiplied by the time taken would confirm the proper radar length of the perimeter is $2 \pi R$ multiplied by the gamma factor. All of this is in line with special relativity in flat spacetime.