Do interference rings disappear in an interferometer if the path lengths are identical?

Question

Consider a standard Michelson Interferometer (I took the picture from http://en.wikipedia.org/wiki/Interferometer)

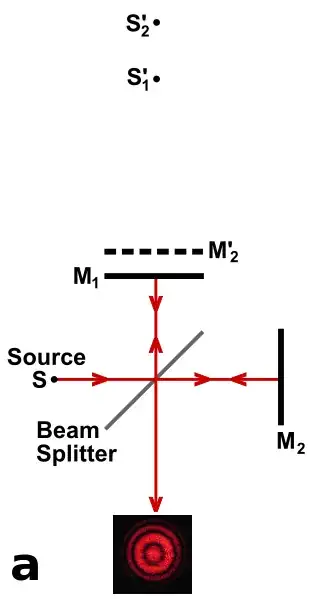
The incident beam is split into two parts, where the two parts travel on different paths to the screen. If the paths are of different length and the incident wave is a spherical one, one sees the interference ring pattern at the detector. I now have three questions:

1.) What happens if the path lengths are exactly identical. Do I then still see the interference pattern?

2.) How does the patter on the screen change if I then slowly change one of the path lengths?

3.) What happens if I use plane waves instead of spherical ones? If the difference between the two paths corresponds to a phase difference of $\Delta \phi= \pi$ do the plane waves cancel out at the screen?

Answer 1

The answer is no, you don't get any interference rings if both arms of the Michelson are identical and the beamsplitter is perfectly flat.

The answer with real optics is somewhat more complicated. Real laser beams have curved wavefronts (as opposed to plane) whose curvature changes as they propagate. If you take two laser beams of the same frequency but different curvatures and overlap them on a camera, then you will get interference rings like shown in your wikipedia diagram, two laser beams of the same curvature give an interference pattern with no rings.

In a Michelson interferometer the things which could cause the two returning beams to have different curvatures are numerous but the most common ones are: path length differences between the arms, curvature of the two end mirrors, or curvature of the beamsplitter.

Answer 2

First consider only the center point of the screen.

• Identical lengths: red dot.
• Length differ by $\lambda/2$: black dot.

Light source is a laser then you can add any natural number of wavelengths to one distance, and still result will be the same. If light source is for example lightbulb with lens making parallel rays and a "pupil" making the beam narrow, then the effect will disappear when difference of lengths is around or grater than length of a single wave packet. If I recall correctly one wave packet from lightbulb has length around $100 {\mu}m$.

Ad 2) Separation of interference fringe will not change, but fringes will gradually move from center or to center.

Ad 3) There will be no interference fringes. Whole screen will have the same intensity as the center point.

Answer 3

In order to not to see the interference patterns you would need a precision of micrometers in the arms distances (order of the laser wave-lengh). If you have this precision in you measurements I would go with the "curved wave-form" explanation, if not, you just don't have the same arm distances: in a very controlled Michelson interferometer the arms are slightly different so one can account for the changes in the interference patters as the mobile arm moves.

Answer 4

You will always have destructive and constructive lines. The best you can do is one of each. The Michelson interferometer produces two images, the one that is usually enlarged and viewed on a screen, the main image. But another image is projected back onto the light source, usually a laser. This image is always the opposite of the other. So if you get total destructive on one screen the other will be constructive. There is no way to get dark in one without getting light in the other.

Answer 5

Whether the centerline path length is identical or differs by a whole number of wavelengths does not matter. You will still get a bright spot in the center. If the setup is perfect as you show, with the beamsplitter exactly at $45^\circ$ and incidence on the mirrors and screen perfectly perpendicular, you will not have any fringes because all lengths do not change. Fig 1 in the Wikipedia article has a sketch that shows the angles not perfect. In that case, the path length will vary over the area and you will see fringes.