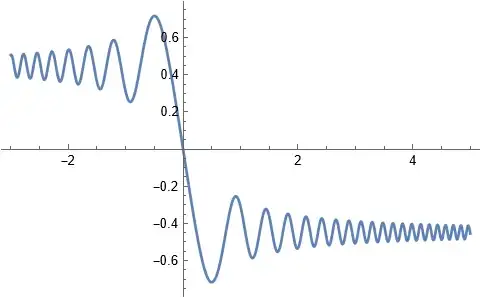
It isn't just the point $t=0$ where the transition rate is strongest, it is the whole region of time where $$|t| \lesssim {\small \frac2\alpha} H_{12} \tag{1}$$
and the reason can indeed be seen from the Bloch sphere:
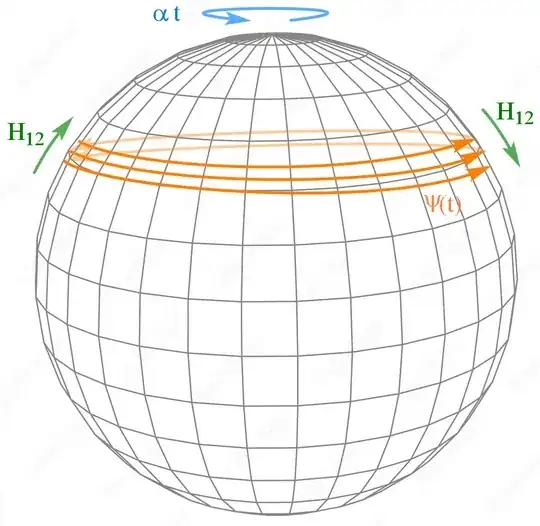
where the part of the Hamiltonian proportional to $\frac{t\alpha}2$ is rotating the state around the sphere's polar axis and the $H_{12}$ part is trying to rotate it around some perpendicular axis. This latter rotation will be ineffective if the first one is much faster, because if $H_{12}$ moves the state to a lower latitude on the right-hand side, then it will be moved back to a higher latitude a short time later, when the state is on the left-hand side, as shown in the picture.
There will only be substantial change in latitude if the rotation around the polar axis is slower than that caused by $H_{12}$, i.e. when $(1)$ holds. And even then we need $H_{12}$ to be strong enough to give a large rotation angle in that limited interval, so we need:
$$\frac{|H_{12}|^2}\alpha \gtrsim 1 \tag{2}$$
The way to solve it mathematically is of course to go to the interaction picture (see below) which means we look at the Bloch sphere from a rotating frame, in this case not uniformly rotating but with rotation speed proportional to $t\alpha$. Trajectories on the Bloch sphere will then look like the examples sketched here:
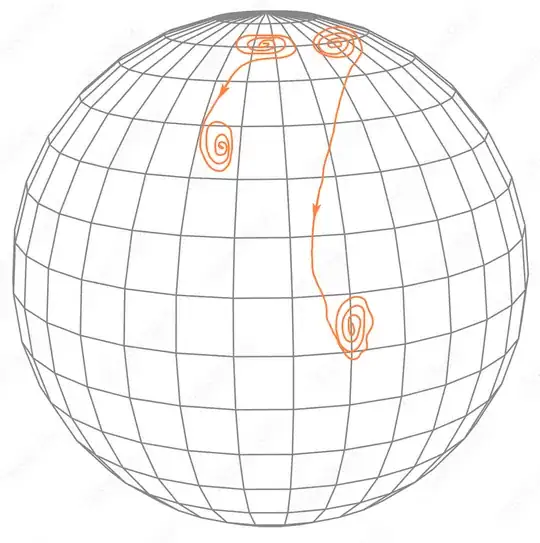
where we will most of the time have the state spiraling around in a very small region, only making a substantial move in the aforementioned time interval around $t=0$. The precise trajectory depends on the starting point and the values of the parameters. In equations, if the interaction picture state is called $|\phi\rangle$ instead of $|\psi\rangle$, we get:
$$
\begin{bmatrix} \phi_+(t) \\ \phi_-(t) \end{bmatrix}
=
\begin{bmatrix} e^{\,i\alpha\,t^2\!/4}\ \psi_+(t) \\ e^{-i\alpha\,t^2\!/4}\ \psi_-(t) \end{bmatrix}
$$
and the time dependence now is:
$$
i\,\frac{d}{dt}\begin{bmatrix} \phi_+(t) \\ \phi_-(t) \end{bmatrix}
=
\begin{bmatrix} 0 & e^{\,i\alpha\,t^2\!/2}H_{12} \\
e^{-i\alpha\,t^2\!/2}H^{^{\displaystyle *}}_{12}& 0 \end{bmatrix}
\begin{bmatrix} \phi_+(t) \\ \phi_-(t) \end{bmatrix}$$
where the mixing of the elements of $|\phi\rangle$ only takes place when $t$ is close enough to $0$, because the matrix elements are vastly fluctuating for $t$ far away from $0$. So this is in fact a clear case of decoherence.
Actually Mathematica gives an analytical solution in terms of the hypergeometric $\!\ _{1\!}F_1$, but it looks a bit asymmetric. Checking it for errors is left as an exercise for the reader:
$$ \begin{align}
\phi_+(t) &=\
_{1\!}F_1\Big(\!{\small \frac{i |H_{12}|^2}{2 \alpha};\frac{1}{2};\frac{i \alpha t^2}{2}
\!}\Big)\, \phi_+(0) \ -it H_{12}^{\ }
\ _{1\!}F_1\Big(\!{\small \frac{\alpha+i |H_{12}|^2}{2 \alpha};\frac{3}{2};\frac{i \alpha t^2}{2} \!}\Big)\,\phi_-(0)
\\[10pt]
\phi_-(t) &= e^{-i\alpha t^2\!/2}\Big[
\!\! -\! it H^{^{\displaystyle *}}_{12}
\ _{1\!}F_1\Big(\!{\small \frac{2\alpha\!+\!i |H_{12}|^2}{2 \alpha};\frac{3}{2};\frac{i \alpha t^2}{2}
\!} \Big)\, \phi_+(0)
+\!\!\ _{1\!}F_1\Big(\!{\small \frac{\alpha\!+\!i |H_{12}|^2}{2 \alpha};\frac{1}{2};\frac{i \alpha t^2}{2}\!} \Big)\,\phi_-(0) \Big]
\end{align} $$
=== EDIT: ===
I think the Mathematica answer is correct, and it can indeed be written in an equivalent, but more symmetric form by simplifying the second line:
$$ \begin{align}
\phi_+(t) &=\
_{1\!}F_1\Big(\!{\small \frac{i |H_{12}|^2}{2 \alpha};\frac{1}{2};\frac{i \alpha t^2}{2}
\!}\Big)\, \phi_+(0) \ -it H_{12}^{\ }
\ _{1\!}F_1\Big(\!{\small \frac{\alpha+i |H_{12}|^2}{2 \alpha};\frac{3}{2};\frac{i \alpha t^2}{2} \!}\Big)\,\phi_-(0)
\\[10pt]
\phi_-(t) &= -\! it H^{^{\displaystyle *}}_{12}
\ _{1\!}F_1\Big(\!{\small \frac{\alpha\!-\!i |H_{12}|^2}{2 \alpha};\frac{3}{2};\frac{-i \alpha t^2}{2}
\!} \Big)\, \phi_+(0)
+\!\!\ _{1\!}F_1\Big(\!{\small \frac{-i |H_{12}|^2}{2 \alpha};\frac{1}{2};\frac{-i \alpha t^2}{2}\!} \Big)\,\phi_-(0)
\end{align} $$
Plotting it on the Bloch sphere gives the following, for $|\psi\rangle$ and $|\phi\rangle$ respectively, with parameters $H_{12}=1, \alpha=10,$ and $\phi(0)=\frac1{\sqrt 2} \binom{1}{-i},$ plotted for $t=-3\dots 5$
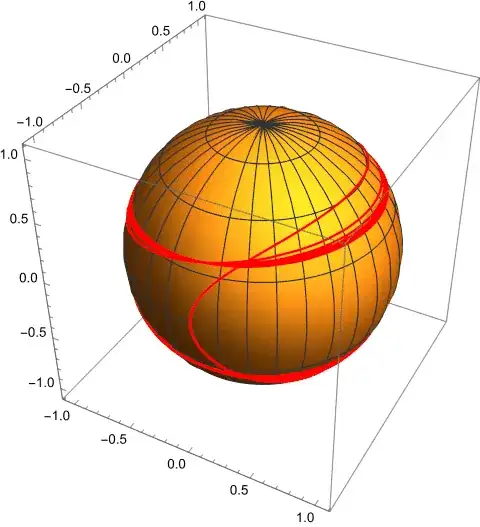
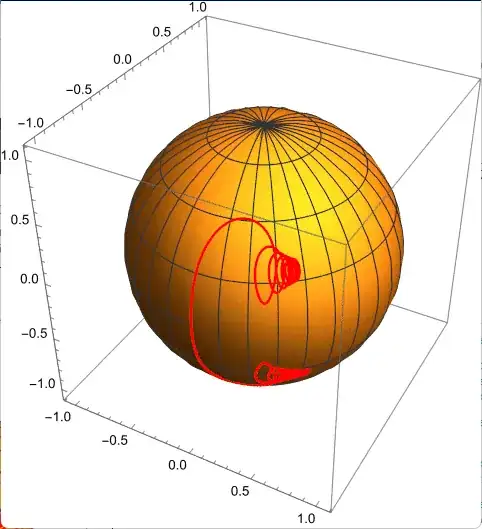
As can be seen from the image, in the early and late "spiraling era" for $|\phi\rangle$, there is not only spiraling, but also some drift in the longitude on the sphere. I missed that in my sketch above! For the transition of the amplitudes it doesn't really matter, the amplitude ratio $\psi_+/\psi_-$ is purely determined by the latitude, which looks like this: