Evaporation can be easily understood from the Maxwell-Boltzamann distribution. There is always a finite number of high speed atoms/molecules, however small, which have the energy to leave.
Solids do not obey Maxwell-Botzmann distribution because the motion of their atoms/molecules is highly correlated. That is why most solids do not sublimate.
What, then, is the mechanism of sublimation? How do some atoms/molecules preferentially gather the energy to escape?
As pointed out correctly by Chemomechanics in their comments above, the more tightly-bound the surface atoms of a solid are, the lower we expect the vapor pressure to be and hence the lower the rate of sublimation. As a thermally-activated process, we also expect the sublimation rate to rise with rising temperatures.
That is why most solids do not sublimate.
I'll question the premise here, as all solids do sublimate. That is, all matter has a nonzero vapor pressure at nonzero temperature, which is any temperature. Consider a chart of element vapor pressures:
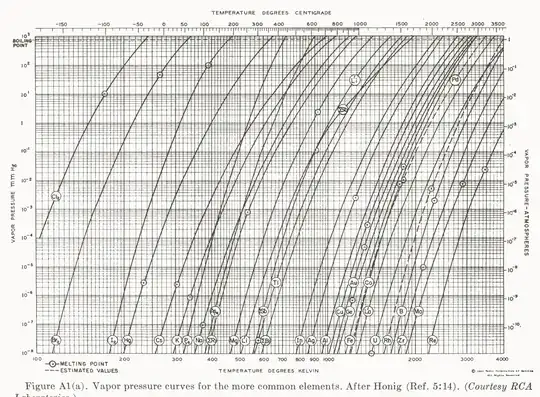
Notably, the elements are ordered essentially according to how refractory they are—i.e., their melting/boiling temperatures. In turn, we know these material properties depend strongly on the bonding strength in the condensed state.
Further, the slopes are all nearly identical in this presentation, indicating that the temperature—along with the bonding strength—mediates the vapor pressure, and exponentially so.
This is all a good match to the Arrhenius model for thermally activated processes: The evaporation rate can be modeled as scaling with $\exp(-E/kT)$, where $E$ is a relevant activation energy to be overcome. For sublimation, this barrier corresponds to the enthalpy of sublimation, or detachment from the solid state into the gas state, which reflects the bonding strength.
A microscopic view is that in condensed matter (as with gases) there is a high-energy tail of the particle distribution. Can the distribution be modeled as Maxwell–Boltzmann? Previous discussions: 1, 2, 3. To summarize (poorly), the distribution is in some sense unchanged in the condensed state, but models relying on it may be more or less effective because of the interactions present. In the literature, Pregenzer and Suhl's "Validity of Brownian-motion theory of activated processes: Sublimation" discusses when the use of the exact Maxwell–Boltzmann distribution is likely to be effective or ineffective for modeling sublimation under different conditions.
A macroscopic view is that upon sublimation, detachment of atoms/molecules increases their configurational entropy, but the required enthalpy of sublimation cools the surroundings, decreasing their thermal entropy. Nature of course tends to maximize total entropy, and for systems in thermal and mechanical contact with their surroundings (like a sublimating solid), this implies minimization of the Gibbs free energy $G\equiv H-TS$. The opposition between the $-TS$ and $H$ terms corresponds to the entropy tradeoffs described above. At higher temperatures, the appearance of $T$ in the $-TS$ term means that the gas state is always favored, and in fact the tendency is exponential, as specified in the Arrhenius model.
Both views are consistent with sublimation of solids at any temperature, although the rate is smaller—certainly negligible for most solids around us—with decreasing temperature, increasing boiling temperature, and increasing partial pressure of that material already in the gas phase.
