Getting Non-Simultaneous Results for a Galilean Transformation of the Lightbulbs in a Train Issue

Question

I am reading Relativity, Gravitation, and Cosmology: A Basic Introduction by TA-PEI CHENG.

He discusses an example of light bulbs on a moving train in section 2.2.2, "Relativity of Simultaneity—the New Kinematics." This example regards the simultaneity of events.

I tried to play with the example myself and found that under the following considerations, I get non-simultaneous events even in non-Lorentzian transformations. Apparently, the events need to be simultaneous. I am interested in knowing what consideration here is faulty. Here is my work:

Example begins:

Two light bulbs are at distance

L, with an observer standing midway, receiving the light signals at the same time. He then concludes simultaneity of events with $t_1' = t_2' = \frac{L}{2c}$

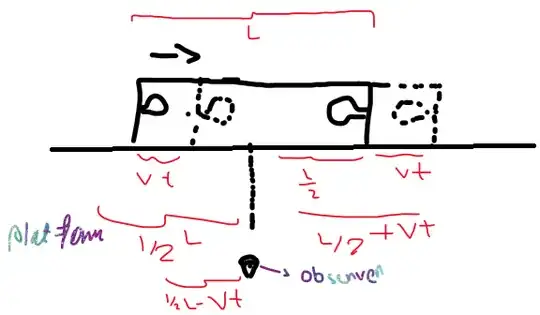
Let these two light bulbs be located at the two ends of a rail car. One observer is at the midpoint on the moving car, and another observer is at the midpoint on the rail platform. The bulbs emit their light signals when the rail car’s middle lines up with the platform observer. The lights then originate at equal distances from the observer. When the light pulses arrive at the observer, this would no longer be the midpoint: one bulb would have moved further away, and the other closer.

$L/2 - vt', L/2 + vt'$

Thus the observer on the platform sees the time intervals:

$\Delta t = \frac{(L/2 + vt') - (L/2 - vt')}{c} = \frac{2vt'}{c} = \frac{2v}{c} \frac{L}{2c} = \frac{v}{c^2} L = \beta \frac{L}{c}$ Of course, $v/c^2$ could be considered as Zero here, but in this case, would not this already imply that it is dependent on the speed of the train?

However, if we consider relativistic effects, we get:

$t_2 - t_1 = \gamma \left(t - \frac{\beta}{c} \frac{L}{2}\right) - \gamma \left(t + \frac{\beta}{c} \frac{L}{2}\right) = -\gamma \frac{\beta}{c} L$

The sign comes from picking the direction of velocity.

Here is a sketch.

Answer 1

For Galilean relativity, replace the lights with a mechanism that throws two rocks toward the center. Put on on the train and one on the station next to the train.

For the one on the train, the two rocks would meet in the middle of the train. For the one on the station, they would meet in the middle of the station. The two middles would be in different places because the train moves while the rocks are in flight. The rocks would move a different speeds because the motion of the train is added to the velocity of the rocks on the train. It all makes sense.

Light doesn't work that way. Both observers see light traveling at the same speed and both see it meeting in the middle. Trying to make sense out of that leads to all the counter intuitive results of special relativity. How can a red light photon be different from a blue light photon?

Answer 2

Let's apply the Galileo transformations directly and see what we get. Remember that:

Let a reference frame $O$ with coordinates $(x,t)$ be such that the positive $x$ direction points to the right. We can introduce another frame $O'$ that moves with velocity $-v$ in the frame of $O$, that is, in the negative $x$ direction. The coordinates in $O'$ are then

$$ x' = x + vt$$ $$ t' = t$$

In your case, the frame $O$ is the train frame and the frame $O'$ is the platform frame, because from the perspective of the train in your sketch, the platform is moving to the left.

Your events in $O$ are the following, with the corresponding coordinates:

• Left photon is sent, $(-L/2,0)$
• Right photon is sent, $(L/2, 0)$
• Left photon arrives in the middle, $(0, L/2c)$
• Right photon arrives in the middle, $(0, L/2c)$

Transforming these is now straightforward. The time coordinates are unchanged by Galilean transformations, and for the $x'$ coordinates we get

• $-L/2$
• $L/2$
• $v(L/2c)$
• $v(L/2c)$

The conclusion we can draw from this is that the left photon travelled with a speed

$$v'_L = \frac{\Delta x'}{\Delta t'} = \frac{v(L/2c) + L/2}{L/2c} = v + c $$

and that the right photon travelled with a speed $v'_R = v - c$, following above. This is the Galilean velocity addition at play, so everything is as expected.